Exam 9: Counting, Probability Distributions, and Further Topics in Probability
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Find the expected value for the random variable.
-A business bureau gets complaints as shown in the following table. Find the expected number of complaints per day.
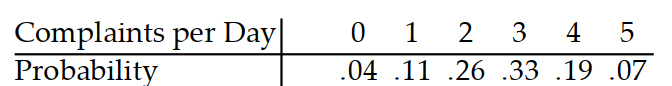
(Multiple Choice)
4.9/5  (29)
(29)
A die is rolled 20 times and the number of twos that come up is tallied. Find the probability of getting the given result.
-Exactly four twos
(Multiple Choice)
4.9/5  (38)
(38)
Provide an appropriate response.
-Consider the following formulas: and .
Given the same values for and in each formula, which is the smaller value, or ?
How does this relate to the concept of counting the number of outcomes based on whether or not order is a criterion?
(Essay)
4.8/5  (42)
(42)
Use the multiplication principle to solve the problem.
-License plates are made using 3 letters followed by 2 digits. How many plates can be made if repetition of letters and digits is allowed?
(Multiple Choice)
4.9/5  (31)
(31)
Find the expected value of the random variable in the experiment.
-A bag contains six marbles, of which four are red and two are blue. Suppose two marbles are chosen at random and represents the number of red marbles in the sample.
(Multiple Choice)
4.8/5  (43)
(43)
Find the expected value for the random variable x having this probability function.
- =5 =6 =7 =8
=5 =6 =7 =8
(Multiple Choice)
4.8/5  (39)
(39)
A bag contains 6 cherry, 3 orange, and 2 lemon candies. You reach in and take 3 pieces of candy at random. Find the probability.
-1 cherry, 2 lemon
(Multiple Choice)
4.8/5  (37)
(37)
Find the requested long-range probabilities based on the transition matrix or data given.
-Tulips with one red and one white gene produce pink tulips. Find the long-range prediction for the fraction of red, pink and white tulips.
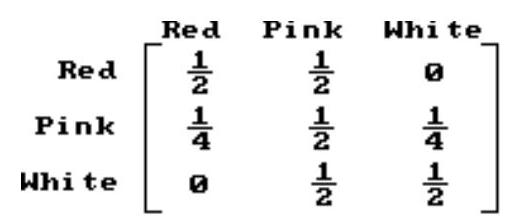
(Multiple Choice)
4.7/5  (39)
(39)
Solve the problem.
-Two student representatives, a treasurer and a secretary, are to be chosen from a group of five students: Andrew, Brenda, Chad, Dorothy, and Eric. In how many different ways can the representatives be chosen if the two must not be the same sex?
(Multiple Choice)
4.9/5  (45)
(45)
Solve the problem.
-Three student representatives, a president, a secretary, and a treasurer, are to be chosen from a group of five students: Andrew, Brenda, Chad, Dorothy, and Eric. In how many different ways can the representatives be chosen if the president must be a woman and the secretary and treasurer must be men?
(Multiple Choice)
5.0/5  (39)
(39)
Prepare a payoff matrix
-A farmer must decide on which of two pieces of land to grow his crops. The first piece of land has better soil and will yield a larger harvest. However this piece of land is low lying and is coastal and his crops will be destroyed in the event of a storm and flooding. The second piece of land has poorer soil but is at a higher elevation and would not be affected by flooding. If he uses the low-lying piece of land and there is no flooding he will make a profit of . If he uses the low-lying piece of land and there is flooding, he will lose . If he uses the higher piece of land and there is no flooding, he will make a profit of . If he uses the higher piece of land and there is flooding, he will make a profit of . (If there is flooding there will be a smaller supply of the crop and his profit will be higher). Prepare a payoff matrix.
(Multiple Choice)
4.7/5  (31)
(31)
Provide an appropriate response.
-In the context of Markov chains, explain why the matrix below could not be a transition matrix.
(Essay)
4.8/5  (32)
(32)
Find the requested probability.
-What is the probability that 16 rolls of a fair die will show 5 fours?
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-10 people are bowling: 2 use a black ball and 8 use a blue ball. How many different black and blue bowling ball sequences can occur on the rack?
(Multiple Choice)
4.9/5  (41)
(41)
Provide an appropriate response.
-In the context of Markov chains, explain why the matrix below could not be a transition matrix.
(Essay)
4.7/5  (39)
(39)
Solve the problem.
-Suppose 6 people sit at a circular table. Find the probability that 2 particular people are sitting next to each other.
(Multiple Choice)
4.8/5  (38)
(38)
Showing 121 - 140 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)