Exam 6: Inference for Means and Proportions
Exam 1: Collecting Data68 Questions
Exam 2: Describing Data125 Questions
Exam 3: Confidence Intervals148 Questions
Exam 4: Hypothesis Tests119 Questions
Exam 5: Approximating With a Distribution74 Questions
Exam 6: Inference for Means and Proportions166 Questions
Exam 7: Chi-Square Tests for Categorical Variables47 Questions
Exam 8: Anova to Compare Means52 Questions
Exam 9: Inference for Regression123 Questions
Exam 10: Multiple Regression72 Questions
Exam 11: Probability Basics165 Questions
Select questions type
Use the following
In 2005, the average score on the Mathematics portion of the ACT for males was 21.3 with standard deviation 5.3. The average score on the Mathematics portion of the ACT for females was 20.2 with standard deviation 4.8.
-If random samples are taken with 120 males and 105 females, find the mean and standard error of the distribution of differences in sample means, 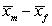 , where
, where 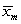 and
and 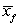 represents the sample means for males and females, respectively. Report your standard error with four decimal places.
represents the sample means for males and females, respectively. Report your standard error with four decimal places.
(Essay)
4.7/5  (43)
(43)
Use the following
Students in a small statistics class were asked to count the number of scars both on their "dominant"
hand (the one they use most often) and on their "off"
hand. The summary statistics are provided. It is of interest to compare the average number of scars on the dominant and off hands.
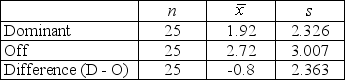 -Construct a 90% confidence interval for the difference in mean number of scars on dominant and off hands. Round your margin of error to two decimal places.
-Construct a 90% confidence interval for the difference in mean number of scars on dominant and off hands. Round your margin of error to two decimal places.
(Essay)
4.8/5  (42)
(42)
Use the following
In a survey conducted by the Gallup organization September 6-9, 2012, 1,017 adults were asked "In general, how much trust and confidence do you have in the mass media - such as newspapers, TV, and radio - when it comes to reporting the news fully, accurately, and fairly?"
Of the 1,017 respondents, 214 said they had "no confidence at all."
-What sample size is needed to reduce the margin of error to 1%?
(Essay)
4.8/5  (40)
(40)
Use the following
Consider taking random samples of size 100 from Population A with mean 85 and standard deviation of 15 and random samples of size 60 from Population B with mean 78 and standard deviation 12.
-Find the mean of the distribution of differences in sample means, . 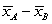
(Multiple Choice)
5.0/5  (39)
(39)
Use the following
For each of the following, find the mean and standard error of the distribution of sample means. Use two decimal places when reporting your standard error.
-Samples of size 15 from a population with mean 25 and standard deviation 4.
(Essay)
4.9/5  (42)
(42)
Use the following
As part of a course project, a statistics student surveyed random samples of 50 student athletes and 50 student non-athletes at his university, with the goal of comparing the heights of the two groups. His summary statistics are displayed in the provided table.
 -Which data analysis method is more appropriate in this situation: paired data difference in means or difference in means with two separate groups? Explain briefly.
-Which data analysis method is more appropriate in this situation: paired data difference in means or difference in means with two separate groups? Explain briefly.
(Essay)
4.9/5  (38)
(38)
Use the following
Turkey is a staple at most traditional Thanksgiving dinners. A random sample of 12 grocery store customers were asked about the size of the turkey they were purchasing for Thanksgiving. The average weight was 13.9 pounds with a standard deviation of 2.2 pounds. The boxplot displays the distribution of the sample turkey weights.
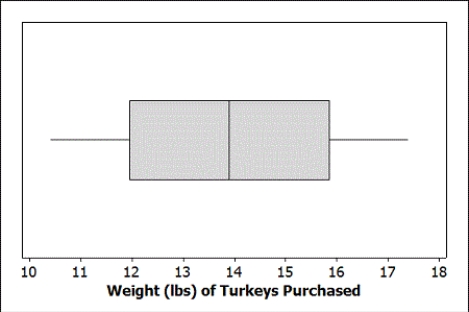 -Is is reasonable to use the t-distribution to construct a confidence interval for the average weight of turkeys purchased at this store? Explain briefly.
-Is is reasonable to use the t-distribution to construct a confidence interval for the average weight of turkeys purchased at this store? Explain briefly.
(Essay)
4.9/5  (34)
(34)
Use the following
In 2012 the Centers for Disease Control and Prevention reported that in a sample of 4,349 African Americans 31% were Vitamin D deficient. Overall, it is believed that Vitamin D deficiency affects 8% of all U.S. adults.
-Test, at the 1% significance level, if this sample provides evidence that the rate of Vitamin D deficiency among African Americans differs significantly from the overall rate of 8%. Include all of the details of the test.
(Essay)
4.8/5  (37)
(37)
Use the following
Turkey is a staple at most traditional Thanksgiving dinners. A random sample of 12 grocery store customers were asked about the size of the turkey they were purchasing for Thanksgiving. The average weight was 13.9 pounds with a standard deviation of 2.2 pounds. The boxplot displays the distribution of the sample turkey weights.
 -Construct a 99% confidence interval for the average weight of turkeys purchased at this store. Round your margin of error to two decimal places.
-Construct a 99% confidence interval for the average weight of turkeys purchased at this store. Round your margin of error to two decimal places.
(Essay)
4.8/5  (38)
(38)
Use the following
Consider taking random samples of size 50 from Population A with mean 15 and standard deviation 3 and random samples of size 75 from Population B with mean 10 and standard deviation 5.
-How many degrees of freedom should be used when conducting inference for with samples of this size? 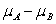
(Multiple Choice)
4.8/5  (36)
(36)
Use the following
A professor with a large introductory statistics class noticed that nearly half of his students missed class the day before a long break (like Thanksgiving Break or Spring Break). He randomly called on students and found 10 students in attendance and 10 students who had skipped class. Later in his office, he examined the current course grades for the 20 students he had selected. A plot of his findings and summary statistics are provided. Note that the grades were entered as proportions, and thus a grade of 0.925 is a 92.5% in the course.
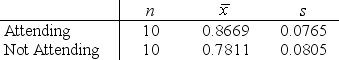
 -Verify that it is reasonable to use a t-distribution to construct a confidence interval, or perform a test about, the difference in mean grades for the two groups of students.
-Verify that it is reasonable to use a t-distribution to construct a confidence interval, or perform a test about, the difference in mean grades for the two groups of students.
(Essay)
4.8/5  (45)
(45)
Use the following
Situations comparing two proportions are described. In each case, determine whether the situation involves comparing proportions for two groups or comparing two proportions from the same group.
-Compare the proportion of U.S. adults who have a positive opinion about the media and the proportion of U.S. adults who have a negative opinion about the media.
(Multiple Choice)
4.8/5  (34)
(34)
Use the following
Suppose that the makers of M&M's claim that 24% of their Milk Chocolate M&M's are blue.
-Assume that the bags of Milk Chocolate M&M's sold in vending machines have 55 candies. Find the mean and standard error of the distribution of sample proportions of blue candies for vending machine bags (i.e., samples of size 55). Use four decimal places when reporting the standard error.
(Essay)
4.8/5  (34)
(34)
Use the following
In an October 2012 survey of 7,786 randomly selected adults living in Germany, 5,840 said they exercised for at least 30 minutes three or more times per week.
-Verify that the sample is large enough to use the normal formula to find a confidence interval for the proportion of Germans who exercises for 30 minutes three or more times a week.
(Essay)
4.9/5  (39)
(39)
Use the following
For each of the following, assume that the sample is a random sample from a distribution that is reasonably normally distributed and that we are doing inference for a population mean.
-Find endpoints of a t-distribution with 3% beyond them in each tail if the sample has size n = 60.
(Short Answer)
4.8/5  (35)
(35)
Use the following
Consider taking random samples of size 100 from Population A with mean 85 and standard deviation of 15 and random samples of size 60 from Population B with mean 78 and standard deviation 12.
-Find the standard error of the distribution of differences in sample means, . 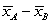
(Multiple Choice)
4.8/5  (33)
(33)
Use the following
A dotplot and the summary statistics for a sample are provided. In each case, indicate whether or not it is appropriate to use the t-distribution.
-n = 15; 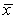 = 44; s = 7.32
= 44; s = 7.32
(Multiple Choice)
4.9/5  (47)
(47)
Use the following
A sample of 148 college students at a large university reports getting an average of 6.85 hours of sleep last night with a standard deviation of 2.12 hours.
-Provide an interpretation of your interval in the context of this data situation.
(Essay)
5.0/5  (44)
(44)
Use the following
A certain species of tree has an average life span of 130 years. A researcher has noticed a large number of trees of this species washing up along a beach as driftwood. She takes core samples from 27 of those trees, selected at random, to count the number of rings and measure the widths of the rings. Counting the rings allows the researcher to determine the age of each tree. The mean age of the sampled driftwood is 119 years old, with standard deviation 46.92 years. The sample data are plotted in the provided dotplot. One of her interests is determining if this sample provides evidence that the average age of the driftwood is less than the 130 year life span expected for this type of tree. If the average age is less than 130 years it might suggest that the trees have died from unusual causes, such as invasive beetles or logging.
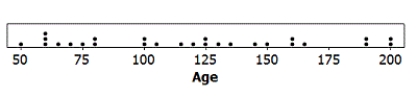 -Verify that it is reasonable to use the t-distribution to perform a test about the average age of driftwood along this beach.
-Verify that it is reasonable to use the t-distribution to perform a test about the average age of driftwood along this beach.
(Essay)
4.8/5  (40)
(40)
Use the following
Consider constructing a 90% confidence interval for 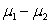 using the sample results
using the sample results 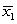 = 103, s1 = 26.4 with n1 = 50 and
= 103, s1 = 26.4 with n1 = 50 and 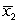 = 96, s2 = 21.1 with n2 = 40.
-What is the t* for the 90% confidence interval?
= 96, s2 = 21.1 with n2 = 40.
-What is the t* for the 90% confidence interval?
(Multiple Choice)
4.8/5  (42)
(42)
Showing 121 - 140 of 166
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)