Exam 16: Regression Models for Nonlinear Relationships
Exam 1: Statistics and Data102 Questions
Exam 2: Tabular and Graphical Methods123 Questions
Exam 3: Numerical Descriptive Measures152 Questions
Exam 4: Introduction to Probability148 Questions
Exam 5: Discrete Probability Distributions158 Questions
Exam 6: Continuous Probability Distributions143 Questions
Exam 7: Sampling and Sampling Distributions136 Questions
Exam 8: Interval Estimation131 Questions
Exam 9: Hypothesis Testing116 Questions
Exam 10: Statistical Inference Concerning Two Populations131 Questions
Exam 11: Statistical Inference Concerning Variance120 Questions
Exam 12: Chi-Square Tests120 Questions
Exam 13: Analysis of Variance120 Questions
Exam 14: Regression Analysis140 Questions
Exam 15: Inference With Regression Models125 Questions
Exam 16: Regression Models for Nonlinear Relationships118 Questions
Exam 17: Regression Models With Dummy Variables130 Questions
Exam 18: Time Series and Forecasting125 Questions
Exam 19: Returns, Index Numbers, and Inflation120 Questions
Exam 20: Nonparametric Tests120 Questions
Select questions type
The cubic regression model allows for ________ change(s) in slope.
Free
(Short Answer)
4.9/5  (31)
(31)
Correct Answer:
two
In which of the following models does the slope coefficient b1 measure the approximate percentage change in  when x increases by 1%?
when x increases by 1%?
Free
(Multiple Choice)
4.7/5  (31)
(31)
Correct Answer:
D
Thirty employed single individuals were randomly selected to examine the relationship between their age (Age) and their credit card debt (Debt) expressed as a percentage of their annual income. Three polynomial models were applied and the following table summarizes Excel's regression results. 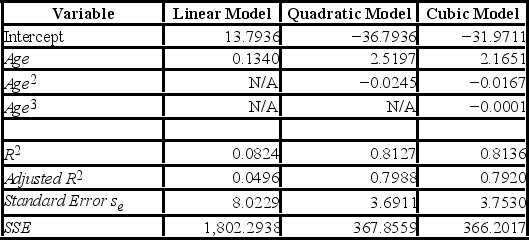 For the cubic model, Debt = β0+ β1Age + β2Age2+ β3Age3+ ε, the following Excel partial output is available. What is the conclusion when testing the individual significance of Age3?
For the cubic model, Debt = β0+ β1Age + β2Age2+ β3Age3+ ε, the following Excel partial output is available. What is the conclusion when testing the individual significance of Age3? 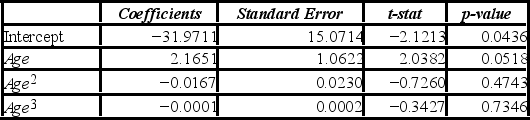
Free
(Essay)
4.9/5  (39)
(39)
Correct Answer:
Do not reject H0: β3 = 0; we cannot conclude Age3 is significant. We cannot conclude that the cubic model is better than the quadratic model.
To compute the coefficient of determination R2 we have to use Excel's ________ function first to compute the correlation between y and  .
.
(Short Answer)
4.7/5  (34)
(34)
The scatterplot shown below represents a typical shape of a cubic regression model y = β0 + β1x + β2x2 + β3x3 + ε. 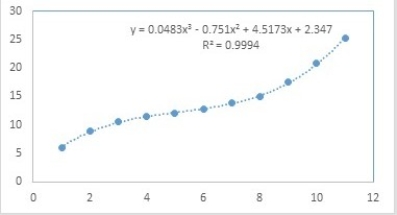 Which of the following is a predicted value
Which of the following is a predicted value  if x is equal to 12?
if x is equal to 12?
(Multiple Choice)
5.0/5  (33)
(33)
The curve representing the regression equation  = b0 + b1x + b2x2 has a U-shape if b2 < 0.
= b0 + b1x + b2x2 has a U-shape if b2 < 0.
(True/False)
4.9/5  (35)
(35)
Typically, the sales volume declines with an increase of a product price. It has been observed, however, that for some luxury goods the sales volume may increase when the price increases. The following scatterplot illustrates this rather unusual relationship. 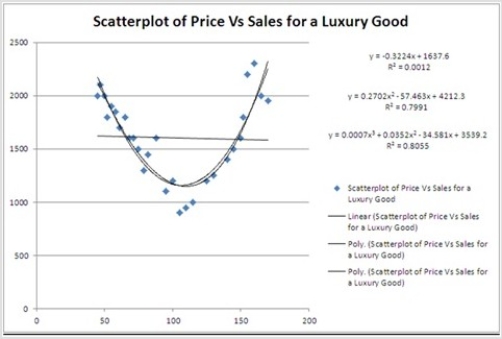 For which of the following two prices are the sales predicted by the quadratic regression equation equal 1700 units?
For which of the following two prices are the sales predicted by the quadratic regression equation equal 1700 units?
(Multiple Choice)
4.8/5  (37)
(37)
The fit of the regression equations 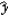 = b0 + b1x + b2x2 and
= b0 + b1x + b2x2 and 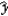 = b0 + b1x + b2x2 + b3x3 can be compared using the coefficient of determination R2.
= b0 + b1x + b2x2 + b3x3 can be compared using the coefficient of determination R2.
(True/False)
4.9/5  (32)
(32)
For the exponential model ln(y) = β0 + β1x + ε, if x increases by one unit, then E(y) changes by approximately
(Multiple Choice)
4.7/5  (39)
(39)
Typically, the sales volume declines with an increase of a product price. It has been observed, however, that for some luxury goods the sales volume may increase when the price increases. The following scatterplot illustrates this rather unusual relationship. 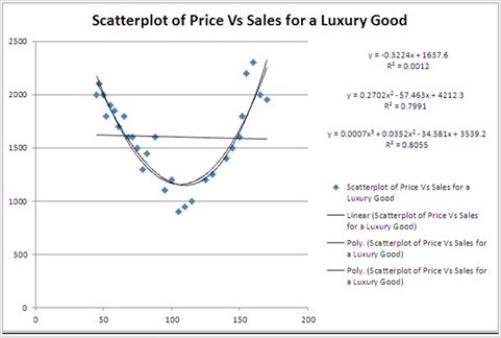 For the considered range of the price, the relationship between Price and Sales should be described by a ________.
For the considered range of the price, the relationship between Price and Sales should be described by a ________.
(Multiple Choice)
4.9/5  (27)
(27)
For the quadratic equation  = b0 + b1x + b2x2, which of the following expressions must be zero in order to minimize or maximize the predicted y?
= b0 + b1x + b2x2, which of the following expressions must be zero in order to minimize or maximize the predicted y?
(Multiple Choice)
4.9/5  (34)
(34)
The logarithmic and log-log models, y = β0 + β1ln(x) + ε and ln(y) = β0 + β1 ln(x) + ε, were fit given data on y and x, and the following table summarizes the regression results. Which of the two models provides a better fit? 
(Multiple Choice)
4.8/5  (41)
(41)
Although allowing for nonlinear trends, polynomials are still linear in the ________.
(Multiple Choice)
4.9/5  (32)
(32)
Which of the following regression models is most likely to provide the best fit for the data represented by the following scatterplot? 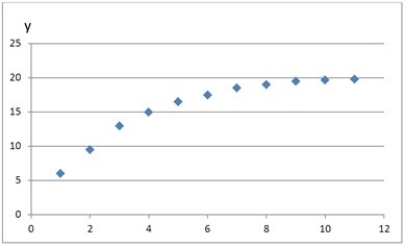
(Multiple Choice)
4.7/5  (33)
(33)
What R function is used to fit a quadratic regression model?
(Multiple Choice)
4.8/5  (32)
(32)
The regression model ln(y) = β0 + β1x + ε is called an exponential model.
(True/False)
4.8/5  (34)
(34)
It is believed that the sales volume of one-liter Pepsi bottles depends on the price of the bottle and the price of a one-liter bottle of Coca-Cola. The following data have been collected for a certain sales region. 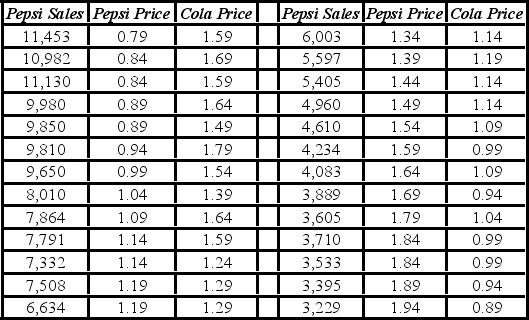 The linear model Pepsi Sales = β0 + β1Pepsi Price + β2Cola Price + ε and the log-log model ln(Pepsi Sales) = β0 + β1ln(Pepsi Price) + β2ln(Cola Price) + ε have been estimated as follows:
The linear model Pepsi Sales = β0 + β1Pepsi Price + β2Cola Price + ε and the log-log model ln(Pepsi Sales) = β0 + β1ln(Pepsi Price) + β2ln(Cola Price) + ε have been estimated as follows:  For the log-log model, interpret the estimated coefficient for ln(Pepsi Price).
For the log-log model, interpret the estimated coefficient for ln(Pepsi Price).
(Essay)
4.7/5  (28)
(28)
The linear and logarithmic models, y = β0 + β1x + ε and y = β0 + β1 ln(x) + ε, were fit given data on y and x, and the following table summarizes the regression results. Which of the two models provides a better fit? 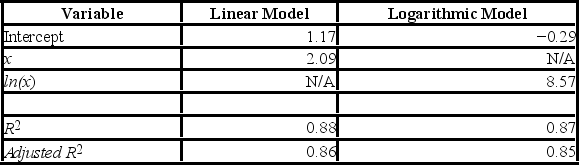
(Multiple Choice)
4.8/5  (28)
(28)
Thirty employed single individuals were randomly selected to examine the relationship between their age (Age) and their credit card debt (Debt) expressed as a percentage of their annual income. Three polynomial models were applied and the following table summarizes Excel's regression results. 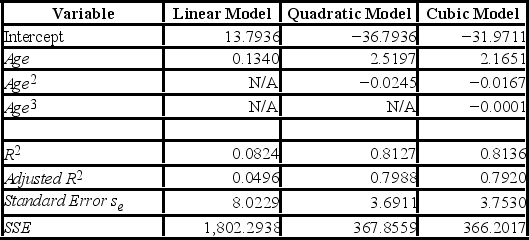 If you impose the restrictions β2 = β3 = 0 on the model Debt = β0 + β1Age + β2Age2 + β3Age3 + ε, what will be the sum of the squared errors (SSER) computed for the restricted model?
If you impose the restrictions β2 = β3 = 0 on the model Debt = β0 + β1Age + β2Age2 + β3Age3 + ε, what will be the sum of the squared errors (SSER) computed for the restricted model?
(Short Answer)
5.0/5  (40)
(40)
It is believed that the sales volume of one-liter Pepsi bottles depends on the price of the bottle and the price of a one-liter bottle of Coca-Cola. The following data have been collected for a certain sales region. 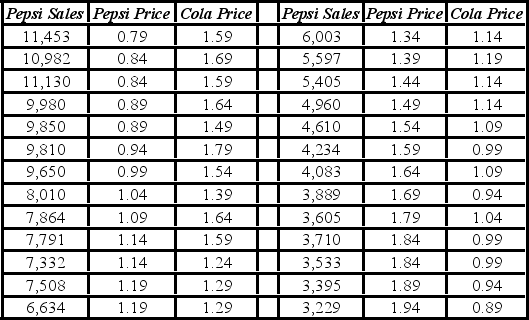 The linear model Pepsi Sales = β0 + β1Pepsi Price + β2Cola Price + ε and the log-log model ln(Pepsi Sales) = β0 + β1ln(Pepsi Price) + β2ln(Cola Price) + ε have been estimated as follows:
The linear model Pepsi Sales = β0 + β1Pepsi Price + β2Cola Price + ε and the log-log model ln(Pepsi Sales) = β0 + β1ln(Pepsi Price) + β2ln(Cola Price) + ε have been estimated as follows:  Using Excel or R, which of the two models provides a better fit?
Using Excel or R, which of the two models provides a better fit?
(Short Answer)
4.7/5  (34)
(34)
Showing 1 - 20 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)