In which of the following models does the slope coefficient b1/100 measure the approximate percentage change in when x increases by 1%?

A) Linear regression model B) Exponential regression model C) Logarithmic regression model D) Log-log regression model A) Linear regression model B) Exponential regression model C) Logarithmic regression model D) Log-log regression model

For the quadratic regression equation = b0 + b1x + b2x2, the predicted y achieves its optimum (maximum or minimum) when x is ________.

A) -2b2/b1 B) -b1/2b2 C) b1/2b2 D) 2b1/b2 A) -2b2/b1 B) -b1/2b2 C) b1/2b2 D) 2b1/b2

In which of the following models does the slope coefficient b1 × 100 measure the approximate percentage change in when x increases by one unit?

A) Linear regression model B) Exponential regression model C) Logarithmic regression model D) Log-log regression model A) Linear regression model B) Exponential regression model C) Logarithmic regression model D) Log-log regression model

The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models, Demand = β0 + β1Price + β2Price2 + β3Price3 + ε and ln(Demand) = β0 + β1ln(Price) + ε, the following regression results are available. Using the cubic model, which of the following is the predicted demand when the price is $200?

A) 14,378.72 B) 9,201.45 C) 10,764.66 D) 12,499.98 A) 14,378.72 B) 9,201.45 C) 10,764.66 D) 12,499.98

Exam 16: Regression Models for Nonlinear Relationships

Typically, the sales volume declines with an increase of a product price. It has been observed, however, that for some luxury goods the sales volume may increase when the price increases. The following scatterplot illustrates this rather unusual relationship. 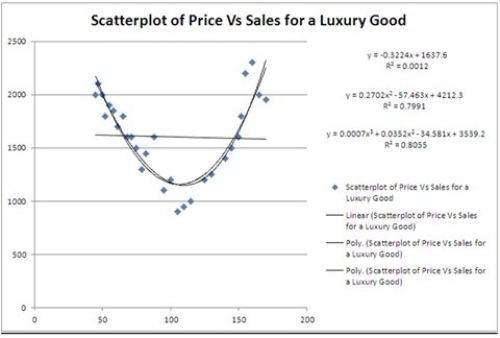For which of the following prices do sales predicted by the quadratic regression equation reach their minimum?

(Multiple Choice)

4.8/5

(33)

Question 41

The following data show the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup. The brewing pot temperature is approximately 180º F. The output for an exponential model, ln(Temp) = β₀ + β₁Time + ε, is below. 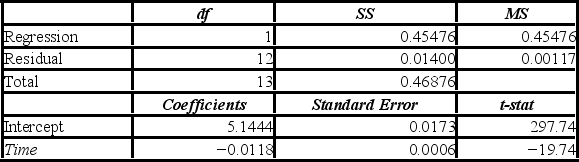Which of the following is the sample correlation coefficient between ln(Temp) and Time?

(Multiple Choice)

4.9/5

(35)

Question 42

A model with one explanatory variable that has been log transformed is called a(n) ________.

(Multiple Choice)

4.8/5

(33)

Question 43

For the logarithmic model y = β₀ + β₁ln(x) + ε, β₁ × 100% is the approximate percentage change in E(y) when x increases by 1%.

(True/False)

4.8/5

(36)

Question 44

In which of the following models does the slope coefficient b₁/100 measure the approximate percentage change in when x increases by 1%?

(Multiple Choice)

4.9/5

(34)

Question 45

Which of the following is not a semi-log regression model?

(Multiple Choice)

4.8/5

(35)

Question 46

For a quadratic regression model , it is important to evaluate the estimated ________ effect of the explanatory variable x on the predicted value of the response variable .

(Short Answer)

4.8/5

(32)

Question 47

Which of the following regression models is a first-order polynomial?

(Multiple Choice)

4.8/5

(38)

Question 48

Typically, the sales volume declines with an increase of a product's price. It has been observed, however, that for some luxury goods the sales volume may increase when the price increases. The following scatterplot illustrates this rather unusual relationship. 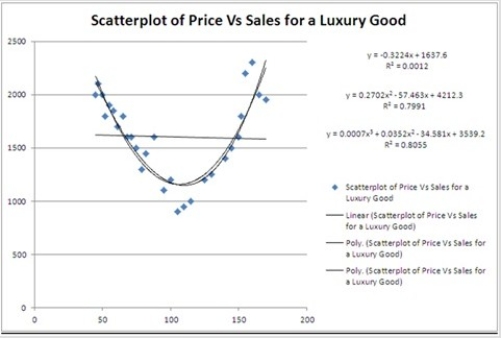Using the quadratic equation, predict the sales if the luxury good is priced at $100.

(Multiple Choice)

4.9/5

(28)

Question 49

It is believed that the sales volume of one-liter Pepsi bottles depends on the price of the bottle and the price of a one-liter bottle of Coca-Cola. The following data have been collected for a certain sales region. 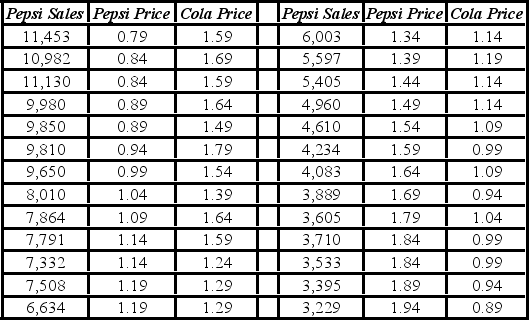The linear model Pepsi Sales = β₀ + β₁Pepsi Price + β₂Cola Price + ε and the log-log model ln(Pepsi Sales) = β₀ + β₁ln(Pepsi Price) + β₂ln(Cola Price) + ε have been estimated as follows: Using Excel or R,what is the percentage of variations in the Pepsi Sales as explained by the log-log model?

(Short Answer)

4.9/5

(38)

Question 50

For the quadratic regression equation = b₀ + b₁x + b₂x², the predicted y achieves its optimum (maximum or minimum) when x is ________.

(Multiple Choice)

4.9/5

(39)

Question 51

Typically, the sales volume declines with an increase of a product price. It has been observed, however, that for some luxury goods the sales volume may increase when the price increases. The following scatterplot illustrates this rather unusual relationship. 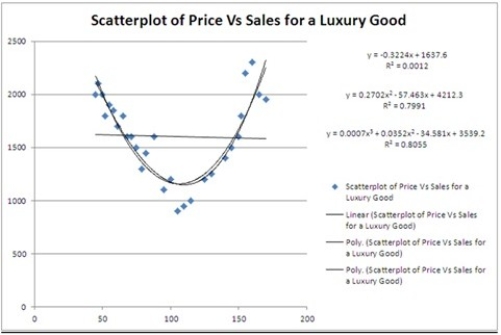What is the number of estimated coefficients of the cubic regression model?

(Multiple Choice)

4.9/5

(30)

Question 52

In which of the following models does the slope coefficient b₁ × 100 measure the approximate percentage change in when x increases by one unit?

(Multiple Choice)

4.9/5

(37)

Question 53

To compute the coefficient of determination R² we have to use R's ________ function first to compute the correlation between y and .

(Short Answer)

4.8/5

(33)

Question 54

It is believed that the sales volume of one-liter Pepsi bottles depends on the price of the bottle and the price of a one-liter bottle of Coca-Cola. The following data have been collected for a certain sales region. 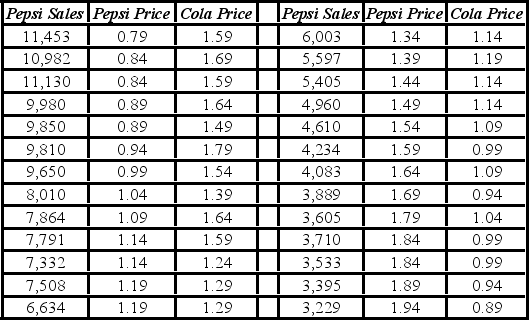The linear model Pepsi Sales = β₀ + β₁Pepsi Price + β₂Cola Price + ε and the log-log model ln(Pepsi Sales) = β₀ + β₁ln(Pepsi Price) + β₂ln(Cola Price) + ε have been estimated as follows: Using the linear model and holding Cola Price constant, what is the predicted change in the Pepsi Sales if the Pepsi Price increases by 10 cents?

(Essay)

4.9/5

(32)

Question 55

An inverted U-shaped curve is also known as ________.

(Multiple Choice)

4.8/5

(35)

Question 56

A model in which the response variable has been log transformed is called a(n) ________.

(Multiple Choice)

4.8/5

(41)

Question 57

Which of the following is a quadratic regression equation?

(Multiple Choice)

4.9/5

(35)

Question 58

The following data show the demand for an airline ticket dependent on the price of this ticket. 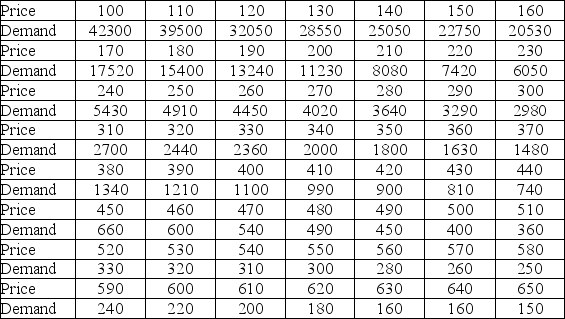For the assumed cubic and log-log regression models, Demand = β₀ + β₁Price + β₂Price²+ β₃Price³+ ε and ln(Demand) = β₀ + β₁ln(Price) + ε, the following regression results are available. 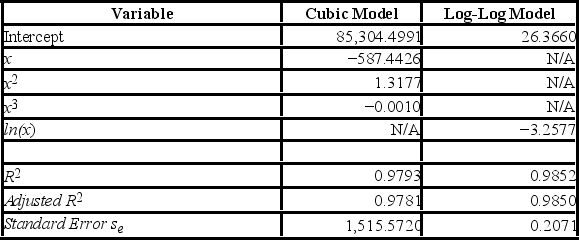Using the cubic model, which of the following is the predicted demand when the price is $200?

(Multiple Choice)

4.7/5

(34)

Question 59

Thirty employed single individuals were randomly selected to examine the relationship between their age (Age) and their credit card debt (Debt) expressed as a percentage of their annual income. Three polynomial models were applied and the following table summarizes Excel's regression results. 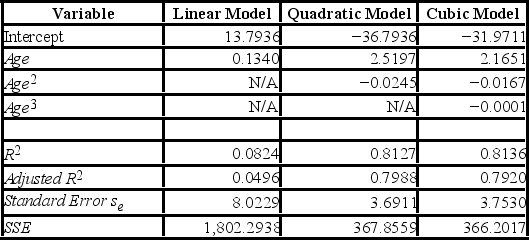What is the predicted percentage debt of a 45-year-old employed single person determined by the model with the best fit?

(Short Answer)

5.0/5

(37)

Question 60

Showing 41 - 60 of 118

A model with one explanatory variable that has been log transformed is called a(n) ________.

For the logarithmic model y = β₀ + β₁ln(x) + ε, β₁ × 100% is the approximate percentage change in E(y) when x increases by 1%.

In which of the following models does the slope coefficient b₁/100 measure the approximate percentage change in when x increases by 1%?

Which of the following is not a semi-log regression model?

For a quadratic regression model , it is important to evaluate the estimated ________ effect of the explanatory variable x on the predicted value of the response variable .

Which of the following regression models is a first-order polynomial?

For the quadratic regression equation = b₀ + b₁x + b₂x², the predicted y achieves its optimum (maximum or minimum) when x is ________.

In which of the following models does the slope coefficient b₁ × 100 measure the approximate percentage change in when x increases by one unit?

To compute the coefficient of determination R² we have to use R's ________ function first to compute the correlation between y and .

An inverted U-shaped curve is also known as ________.

A model in which the response variable has been log transformed is called a(n) ________.

Which of the following is a quadratic regression equation?

Statistics and Data

Tabular and Graphical Methods

Numerical Descriptive Measures

Introduction to Probability

Discrete Probability Distributions

Continuous Probability Distributions

Sampling and Sampling Distributions

Interval Estimation

Hypothesis Testing

Statistical Inference Concerning Two Populations

Statistical Inference Concerning Variance

Chi-Square Tests

Analysis of Variance

Regression Analysis

Inference With Regression Models

Regression Models With Dummy Variables

Time Series and Forecasting

Returns, Index Numbers, and Inflation

Nonparametric Tests

Filters

Exam 16: Regression Models for Nonlinear Relationships

A model with one explanatory variable that has been log transformed is called a(n) ________.

For the logarithmic model y = β0 + β1ln(x) + ε, β1 × 100% is the approximate percentage change in E(y) when x increases by 1%.

In which of the following models does the slope coefficient b1/100 measure the approximate percentage change in when x increases by 1%?

Which of the following is not a semi-log regression model?

For a quadratic regression model , it is important to evaluate the estimated ________ effect of the explanatory variable x on the predicted value of the response variable .

Which of the following regression models is a first-order polynomial?

For the quadratic regression equation = b0 + b1x + b2x2, the predicted y achieves its optimum (maximum or minimum) when x is ________.

In which of the following models does the slope coefficient b1 × 100 measure the approximate percentage change in when x increases by one unit?

To compute the coefficient of determination R2 we have to use R's ________ function first to compute the correlation between y and .

An inverted U-shaped curve is also known as ________.

A model in which the response variable has been log transformed is called a(n) ________.

Which of the following is a quadratic regression equation?

Statistics and Data

Tabular and Graphical Methods

Numerical Descriptive Measures

Introduction to Probability

Discrete Probability Distributions

Continuous Probability Distributions

Sampling and Sampling Distributions

Interval Estimation

Hypothesis Testing

Statistical Inference Concerning Two Populations

Statistical Inference Concerning Variance

Chi-Square Tests

Analysis of Variance

Regression Analysis

Inference With Regression Models

Regression Models With Dummy Variables

Time Series and Forecasting

Returns, Index Numbers, and Inflation

Nonparametric Tests

Filters

For the logarithmic model y = β₀ + β₁ln(x) + ε, β₁ × 100% is the approximate percentage change in E(y) when x increases by 1%.

In which of the following models does the slope coefficient b₁/100 measure the approximate percentage change in when x increases by 1%?

For the quadratic regression equation = b₀ + b₁x + b₂x², the predicted y achieves its optimum (maximum or minimum) when x is ________.

In which of the following models does the slope coefficient b₁ × 100 measure the approximate percentage change in when x increases by one unit?

To compute the coefficient of determination R² we have to use R's ________ function first to compute the correlation between y and .