Exam 7: Sampling and Sampling Distributions
Exam 1: Data and Statistics85 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays112 Questions
Exam 3: Descriptive Statistics: Numerical Measures139 Questions
Exam 4: Introduction to Probability129 Questions
Exam 5: Discrete Probability Distributions150 Questions
Exam 6: Continuous Probability Distributions144 Questions
Exam 7: Sampling and Sampling Distributions119 Questions
Exam 8: Interval Estimation118 Questions
Exam 9: Hypothesis Tests118 Questions
Exam 10: Inference About Means and Proportions With Two Populations127 Questions
Exam 11: Inferences About Population Variances113 Questions
Exam 12: Tests of Goodness of Fit, Independence and Multiple Proportions76 Questions
Exam 13: Experimental Design and Analysis of Variance125 Questions
Exam 14: Simple Linear Regression103 Questions
Exam 15: Multiple Regression109 Questions
Exam 16: Regression Analysis: Model Building82 Questions
Exam 17: Time Series Analysis and Forecasting80 Questions
Exam 18: Nonparametric Methods83 Questions
Exam 19: Statistical Methods for Quality Control75 Questions
Exam 20: Decision Analysis71 Questions
Exam 21: Sample Survey68 Questions
Select questions type
Roger Hall, who oversees six Ford dealerships, believes that the colors chosen by customers who special-order their cars best reflect most customers' true color preferences. For that reason, he has tabulated the color requests specified in a sample of 56 Mustang coupe special orders placed this year. The sample data are listed below.  a. What is the point estimate of the proportion of all Mustang coupe special orders that specify a color preference of black?
b. Describe the sampling distribution of
a. What is the point estimate of the proportion of all Mustang coupe special orders that specify a color preference of black?
b. Describe the sampling distribution of 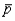 , where
, where 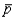 is the proportion of Mustang coupe special orders that specify a color preference of black. Assume that the proportion of all Mustang coupe special orders having a color preference of black is .36.
c. What is the probability that a simple random sample of 56 special orders will provide an estimate of the population proportion of special orders specifying the color black that is within plus or minus .05 of the actual population proportion, assuming p = .36? In other words, what is the probability that
is the proportion of Mustang coupe special orders that specify a color preference of black. Assume that the proportion of all Mustang coupe special orders having a color preference of black is .36.
c. What is the probability that a simple random sample of 56 special orders will provide an estimate of the population proportion of special orders specifying the color black that is within plus or minus .05 of the actual population proportion, assuming p = .36? In other words, what is the probability that 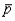 will be between .31 and .41?
will be between .31 and .41?
(Essay)
4.8/5  (40)
(40)
Scores for a standardized test are normally distributed with a mean of 1200 and a standard deviation of 60. A sample of 36 scores is selected.
a.What is the probability that the sample mean will be larger than 1224?
b.What is the probability that the sample mean will be less than 1230?
c.What is the probability that the sample mean will be between 1200 and 1214?
d.What is the probability that the sample mean will be greater than 1200?
e.What is the probability that the sample mean will be larger than 73.46?
(Short Answer)
4.8/5  (31)
(31)
Random samples of size 36 are taken from a process (an infinite population) whose mean and standard deviation are 20 and 15, respectively. The distribution of the population is unknown. The mean and the standard error of the distribution of sample mean are
(Multiple Choice)
4.8/5  (38)
(38)
Ten percent of the items produced by a machine are defective. A random sample of 100 items is selected and checked for defects.
a.Determine the standard error of the proportion.
b.What is the probability that the sample will contain more than 2.5% defective units?
c.What is the probability that the sample will contain more than 13% defective units?
(Short Answer)
4.9/5  (41)
(41)
A sample of 25 observations is taken from a process (an infinite population). The sampling distribution of 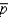 is
is
(Multiple Choice)
5.0/5  (38)
(38)
A sample of 51 observations will be taken from a process (an infinite population). The population proportion equals 0.85. The probability that the sample proportion will be between 0.9115 and 0.946 is
(Multiple Choice)
4.8/5  (35)
(35)
A population has a mean of 84 and a standard deviation of 12. A sample of 36 observations will be taken. The probability that the sample mean will be between 80.54 and 88.9 is
(Multiple Choice)
4.9/5  (33)
(33)
There are 6 children in a family. The number of children defines a population. The number of simple random samples of size 2 (without replacement) which are possible equals
(Multiple Choice)
4.8/5  (37)
(37)
For a population with an unknown distribution, the form of the sampling distribution of the sample mean is
(Multiple Choice)
4.8/5  (32)
(32)
A sample of 24 observations is taken from a population that has 150 elements. The sampling distribution of 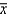 is
is
(Multiple Choice)
4.9/5  (34)
(34)
Which of the following is an example of a nonprobability sampling technique?
(Multiple Choice)
4.9/5  (42)
(42)
The value of the ___________ is used to estimate the value of the population parameter.
(Multiple Choice)
4.7/5  (29)
(29)
The basis for using a normal probability distribution to approximate the sampling distribution of 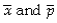 is
is
(Multiple Choice)
4.9/5  (35)
(35)
The fact that the sampling distribution of the sample mean can be approximated by a normal probability distribution whenever the sample size is large is based on the
(Multiple Choice)
4.7/5  (40)
(40)
Exhibit 7-5
Random samples of size 17 are taken from a population that has 200 elements, a mean of 36, and a standard deviation of 8.
-Refer to Exhibit 7-5. The mean and the standard deviation of the sampling distribution of the sample means are
(Multiple Choice)
4.8/5  (27)
(27)
Exhibit 7-5
Random samples of size 17 are taken from a population that has 200 elements, a mean of 36, and a standard deviation of 8.
-There are 8,000 students at the University of Tennessee at Chattanooga. The average age of all the students is 24 years with a standard deviation of 9 years. A random sample of 36 students is selected.
a.Determine the standard error of the mean.
b.What is the probability that the sample mean will be larger than 19.5?
c.What is the probability that the sample mean will be between 25.5 and 27 years?
(Short Answer)
5.0/5  (41)
(41)
Showing 81 - 100 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)