Exam 5: Discrete Probability Distributions

A production process produces 90% non-defective parts. A sample of 10 parts from the production process is selected. a.Define the random variable in words for this experiment. b.What is the probability that the sample will contain 7 non-defective parts? c.What is the probability that the sample will contain at least 4 defective parts? d.What is the probability that the sample will contain less than 5 non-defective parts? e.What is the probability that the sample will contain no defective parts?

Exhibit 5-5 AMR is a computer-consulting firm. The number of new clients that they have obtained each month has ranged from 0 to 6. The number of new clients has the probability distribution that is shown below. 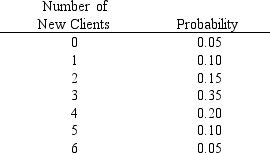-Refer to Exhibit 5-5. The variance is

Exhibit 5-8 The student body of a large university consists of 60% female students. A random sample of 8 students is selected. -Refer to Exhibit 5-8. What is the random variable in this experiment?

Exhibit 5-7 A sample of 2,500 people was asked how many cups of coffee they drink in the morning. You are given the following sample information. -Refer to Exhibit 5-7. The expected number of cups of coffee is

x is a random variable with the probability function: f(x) = x/6 for x = 1,2 or 3. The expected value of x is

Exhibit 5-11 The random variable x is the number of occurrences of an event over an interval of ten minutes. It can be assumed that the probability of an occurrence is the same in any two time periods of an equal length. It is known that the mean number of occurrences in ten minutes is 5.3. -Refer to Exhibit 5-11. The random variable x satisfies which of the following probability distributions?

Exhibit 5-2 The probability distribution for the daily sales at Michael's Co. is given below. -Refer to Exhibit 5-2. The probability of having sales of at least $50,000 is

Ralph's Gas Station is running a giveaway promotion. With every fill-up of gasoline, Ralph gives out a lottery ticket that has a 25% chance of being a winning ticket. Customers who collect four winning lottery tickets are eligible for the "BIG SPIN" for large payoffs. What is the probability of qualifying for the big spin if a customer fills up: (a) 3 times; (b) 4 times; (c) 7 times?

Exhibit 5-9 Forty percent of all registered voters in a national election are female. A random sample of 5 voters is selected. -Refer to Exhibit 5-9. The probability that there are no females in the sample is

Thirty-two percent of the students in a management class are graduate students. A random sample of 5 students is selected. Using the binomial probability function, determine the probability that the sample contains exactly 2 graduate students?

The expected value of a discrete random variable

The key difference between the binomial and hypergeometric distribution is that with the hypergeometric distribution the

Exhibit 5-10 The probability that Pete will catch fish on a particular day when he goes fishing is 0.8. Pete is going fishing 3 days next week. -Excel's POISSON.DIST function has how many inputs?

The student body of a large university consists of 30% Business majors. A random sample of 20 students is selected. a.Define the random variable in words for this experiment. b.What is the probability that among the students in the sample at least 10 are Business majors? c.What is the probability that at least 16 are not Business majors? d.What is the probability that exactly 10 are Business majors? e.What is the probability that exactly 12 are not Business majors?

Exhibit 5-3 The probability distribution for the number of goals the Lions soccer team makes per game is given below. -Refer to Exhibit 5-3. What is the probability that in a given game the Lions will score less than 3 goals?

When sampling without replacement, the probability of obtaining a certain sample is best given by a

Two percent of the parts produced by a machine are defective. Forty parts are selected. Define the random variable x to be the number of defective parts. a.What is the probability that exactly 3 parts will be defective? b.What is the probability that the number of defective parts will be more than 2 but fewer than 6? c.What is the probability that fewer than 4 parts will be defective? d.What is the expected number of defective parts? e.What is the variance for the number of defective parts?

Exhibit 5-11 The random variable x is the number of occurrences of an event over an interval of ten minutes. It can be assumed that the probability of an occurrence is the same in any two time periods of an equal length. It is known that the mean number of occurrences in ten minutes is 5.3. -Refer to Exhibit 5-11. The expected value of the random variable x is

Exhibit 5-4 A local bottling company has determined the number of machine breakdowns per month and their respective probabilities as shown below. -Refer to Exhibit 5-4. The probability of at least 3 breakdowns in a month is

Exhibit 5-10 The probability that Pete will catch fish on a particular day when he goes fishing is 0.8. Pete is going fishing 3 days next week. -When using Excel's POISSON.DIST function, one should choose TRUE for the third input if