Exam 16: Regression Analysis: Model Building
Exam 1: Data and Statistics85 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays112 Questions
Exam 3: Descriptive Statistics: Numerical Measures139 Questions
Exam 4: Introduction to Probability129 Questions
Exam 5: Discrete Probability Distributions150 Questions
Exam 6: Continuous Probability Distributions144 Questions
Exam 7: Sampling and Sampling Distributions119 Questions
Exam 8: Interval Estimation118 Questions
Exam 9: Hypothesis Tests118 Questions
Exam 10: Inference About Means and Proportions With Two Populations127 Questions
Exam 11: Inferences About Population Variances113 Questions
Exam 12: Tests of Goodness of Fit, Independence and Multiple Proportions76 Questions
Exam 13: Experimental Design and Analysis of Variance125 Questions
Exam 14: Simple Linear Regression103 Questions
Exam 15: Multiple Regression109 Questions
Exam 16: Regression Analysis: Model Building82 Questions
Exam 17: Time Series Analysis and Forecasting80 Questions
Exam 18: Nonparametric Methods83 Questions
Exam 19: Statistical Methods for Quality Control75 Questions
Exam 20: Decision Analysis71 Questions
Exam 21: Sample Survey68 Questions
Select questions type
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed. 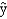 = 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. If we want to test for the significance of the model, the critical value of F at 95% confidence is
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. If we want to test for the significance of the model, the critical value of F at 95% confidence is
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
C
What value of Durbin-Watson statistic indicates no autocorrelation is present?
Free
(Multiple Choice)
4.8/5  (49)
(49)
Correct Answer:
B
The range of the Durbin-Watson statistic is between
Free
(Multiple Choice)
4.8/5  (24)
(24)
Correct Answer:
D
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed. 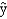 = 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. The test statistic for testing the significance of the model is
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. The test statistic for testing the significance of the model is
(Multiple Choice)
4.7/5  (33)
(33)
A regression model with one independent variable, x1, resulted in an SSE of 50. When a second independent variable, x2, was added to the model, the SSE was reduced to 40. At = 0.05, determine if x2 contributes significantly to the model. The sample size for both models was 30.
(Essay)
4.7/5  (34)
(34)
A variable such as z, whose value is z = x1x2 is added to a general linear model in order to account for potential effects of two variables x1 and x2 acting together. This type of effect is
(Multiple Choice)
4.7/5  (34)
(34)
A regression analysis was applied in order to determine the relationship between a dependent variable and 8 independent variables. The following information was obtained from the regression analysis.R Square = 0.80
SSR = 4,280
Total number of observations n = 56
a.Fill in the blanks in the following ANOVA table.
b.Is the model significant? Let = 0.05. 
(Essay)
4.9/5  (38)
(38)
A regression model relating units sold (y), price (x1), and whether or not promotion was used (x2 = 1 if promotion was used and 0 if it was not) resulted in the following model. 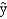 = 120 - 0.03x1 + 0.7x2
and the following information is provided.n = 15 Sb1 = .01 Sb2 = 0.1
a.Is price a significant variable?
b.Is promotion significant?
= 120 - 0.03x1 + 0.7x2
and the following information is provided.n = 15 Sb1 = .01 Sb2 = 0.1
a.Is price a significant variable?
b.Is promotion significant?
(Essay)
5.0/5  (30)
(30)
In a regression analysis involving 18 observations and four independent variables, the following information was obtained.Multiple R = 0.6000
R Square = 0.3600
Standard Error = 4.8000
Based on the above information, fill in all the blanks in the following ANOVA table. 
(Essay)
4.9/5  (33)
(33)
The following are partial results of a regression analysis involving sales (y in millions of dollars), advertising expenditures (x1 in thousands of dollars), and number of salespeople (x2) for a corporation. The regression was performed on a sample of 10 observations. 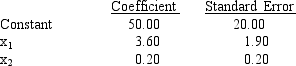 a.At = 0.05, test for the significance of the coefficient of advertising.
b.If the company uses $20,000 in advertisement and has 300 salespersons, what are the expected sales? (Give your answer in dollars.)
a.At = 0.05, test for the significance of the coefficient of advertising.
b.If the company uses $20,000 in advertisement and has 300 salespersons, what are the expected sales? (Give your answer in dollars.)
(Essay)
4.9/5  (39)
(39)
A researcher is trying to decide whether or not to add another variable to his model. He has estimated the following model from a sample of 28 observations. 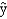 = 23.62 + 18.86x1 + 24.72x2
SSE = 1,425 SSR = 1,326
He has also estimated the model with an additional variable x3. The results are
= 23.62 + 18.86x1 + 24.72x2
SSE = 1,425 SSR = 1,326
He has also estimated the model with an additional variable x3. The results are 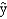 = 25.32 + 15.29x1 + 7.63x2 + 12.72x3
SSE = 1,300 SSR = 1,451
What advice would you give this researcher? Use a .05 level of significance.
= 25.32 + 15.29x1 + 7.63x2 + 12.72x3
SSE = 1,300 SSR = 1,451
What advice would you give this researcher? Use a .05 level of significance.
(Essay)
4.8/5  (35)
(35)
Exhibit 16-4
In a laboratory experiment, data were gathered on the life span (y in months) of 33 rats, units of daily protein intake (x1), and whether or not agent x2 (a proposed life extending agent) was added to the rats diet (x2 = 0 if agent x2 was not added, and x2 = 1 if agent was added.) From the results of the experiment, the following regression model was developed. 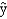 = 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. The multiple coefficient of determination is
= 36 + 0.8x1 - 1.7x2
Also provided are SSR = 60 and SST = 180.
-Refer to Exhibit 16-4. The multiple coefficient of determination is
(Multiple Choice)
4.7/5  (29)
(29)
Exhibit 16-3
Below you are given a partial Excel output based on a sample of 25 observations.  -Refer to Exhibit 16-3. The estimated regression equation is
-Refer to Exhibit 16-3. The estimated regression equation is
(Multiple Choice)
4.8/5  (36)
(36)
Forty-eight observations of a dependent variable (y) and five independent variables resulted in an SSE of 438. When two additional independent variables were added to the model, the SSE was reduced to 375. At a 5% level of significance, determine if the two additional independent variables contribute significantly to the model.
(Essay)
4.8/5  (41)
(41)
A sample of 6 recent college graduates shows their current annual income (in $1000), years of education, and current age (in years). The data follow:  Use Excel's Regression Tool to estimate a general linear model of the form that predicts annual income.
Use Excel's Regression Tool to estimate a general linear model of the form that predicts annual income. 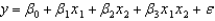
(Essay)
4.7/5  (30)
(30)
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed. 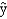 = 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
-Refer to Exhibit 16-1. The test statistic for testing the significance of the model is
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
-Refer to Exhibit 16-1. The test statistic for testing the significance of the model is
(Multiple Choice)
4.8/5  (33)
(33)
Exhibit 16-1
In a regression analysis involving 25 observations, the following estimated regression equation was developed. 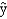 = 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
-Refer to Exhibit 16-1. The coefficient of x3
= 10 - 18x1 + 3x2 + 14x3
Also, the following standard errors and the sum of squares were obtained.Sb1 = 3 Sb2 = 6 Sb3 = 7
SST = 4,800 SSE = 1,296
-Refer to Exhibit 16-1. The coefficient of x3
(Multiple Choice)
4.8/5  (27)
(27)
Showing 1 - 20 of 82
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)