Exam 4: Introduction to Probability

Through a telephone survey, a low-interest bank credit card is offered to 400 households. The responses are as follows. 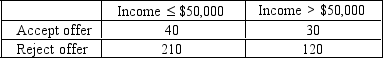a. Develop a joint probability table and show the marginal probabilities.. b. What is the probability of a household whose income exceeds $50,000 and who rejects the offer? c. If income is < $50,000, what is the probability the offer will be accepted? d. If the offer is accepted, what is the probability that income exceeds $50,000?

If A and B are mutually exclusive events with P(A) = 0.3 and P(B) = 0.5, then P(A $\cap$ B) =

Assume you are taking two courses this semester (A and B). Based on your opinion, you believe the probability that you will pass course A is 0.835; the probability that you will pass both courses is 0.276. You further believe the probability that you will pass at least one of the courses is 0.981. a.What is the probability that you will pass course B? b.Is the passing of the two courses independent events? Use probability information to justify your answer. c.Are the events of passing the courses mutually exclusive? Explain. d.What method of assigning probabilities did you use?

A(n) __________ is a collection of sample points.

If a penny is tossed four times and comes up heads all four times, the probability of heads on the fifth trial is

Events A and B are mutually exclusive. Which of the following statements is also true?

In a recent survey in a Statistics class, it was determined that only 60% of the students attend class on Fridays. From past data it was noted that 98% of those who went to class on Fridays pass the course, while only 20% of those who did not go to class on Fridays passed the course. a.What percentage of students is expected to pass the course? b.Given that a person passes the course, what is the probability that he/she attended classes on Fridays?

A lottery is conducted using three urns. Each urn contains chips numbered from 0 to 9. One chip is selected at random from each urn. The total number of sample points in the sample space is

A very short quiz has one multiple-choice question with five possible choices (a, b, c, d, and e) and one true or false question. Assume you are taking the quiz but do not have any idea what the correct answer is to either question, but you mark an answer anyway. a.What is the probability that you have given the correct answer to both questions? b.What is the probability that only one of the two answers is correct? c.What is the probability that neither answer is correct? d.What is the probability that only your answer to the multiple-choice question is correct? e.What is the probability that you have only answered the true or false question correctly?

If a coin is tossed three times, the likelihood of obtaining three heads in a row is

There are two more assignments in a class before its end, and if you get an A on at least one of them, you will get an A for the semester. Your subjective assessment of your performance is 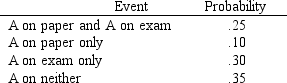a. What is the probability of getting an A on the paper? b. What is the probability of getting an A on the exam? c. What is the probability of getting an A in the course? d. Are the grades on the assignments independent?

In an experiment, events A and B are mutually exclusive. If P(A) = 0.6, then the probability of B

Given that event E has a probability of 0.25, the probability of the complement of event E

All the employees of ABC Company are assigned ID numbers. The ID number consists of the first letter of an employee's last name, followed by four numbers. a.How many possible different ID numbers are there? b.How many possible different ID numbers are there for employees whose last name starts with an "A"?

Assume your favorite football team has 2 games left to finish the season. The outcome of each game can be win, lose or tie. The number of possible outcomes is

Assume you have applied for two scholarships, a Merit scholarship (M) and an Athletic scholarship (A). The probability that you receive an Athletic scholarship is 0.18. The probability of receiving both scholarships is 0.11. The probability of getting at least one of the scholarships is 0.3. a.What is the probability that you will receive a Merit scholarship? b.Are events A and M mutually exclusive? Why or why not? Explain. c.Are the two events, A and M, independent? Explain, using probabilities. d.What is the probability of receiving the Athletic scholarship given that you have been awarded the Merit scholarship? e.What is the probability of receiving the Merit scholarship given that you have been awarded the Athletic scholarship?

In the two upcoming basketball games, the probability that UTC will defeat Marshall is 0.63, and the probability that UTC will defeat Furman is 0.55. The probability that UTC will defeat both opponents is 0.3465. a.What is the probability that UTC will defeat Furman given that they defeat Marshall? b.What is the probability that UTC will win at least one of the games? c.What is the probability of UTC winning both games? d.Are the outcomes of the games independent? Explain and substantiate your answer.

If A and B are independent events with P(A) = 0.05 and P(B) = 0.65, then P(A|B) =

The following probability model describes the number of snowstorms for Washington, D.C. for a given year: 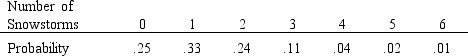The probability of 7 or more snowstorms in a year is 0. a. What is the probability of more than 2 but less than 5 snowstorms? b. Given this a particularly cold year (in which 2 snowstorms have already been observed), what is the conditional probability that 4 or more snowstorms will be observed? c. If at the beginning of winter there is a snowfall, what is the probability of at least one more snowstorm before winter is over?

Of five letters (A, B, C, D, and E), two letters are to be selected at random. How many possible selections are there?