Exam 8: Interval Estimation
Exam 1: Data and Statistics85 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays112 Questions
Exam 3: Descriptive Statistics: Numerical Measures139 Questions
Exam 4: Introduction to Probability129 Questions
Exam 5: Discrete Probability Distributions150 Questions
Exam 6: Continuous Probability Distributions144 Questions
Exam 7: Sampling and Sampling Distributions119 Questions
Exam 8: Interval Estimation118 Questions
Exam 9: Hypothesis Tests118 Questions
Exam 10: Inference About Means and Proportions With Two Populations127 Questions
Exam 11: Inferences About Population Variances113 Questions
Exam 12: Tests of Goodness of Fit, Independence and Multiple Proportions76 Questions
Exam 13: Experimental Design and Analysis of Variance125 Questions
Exam 14: Simple Linear Regression103 Questions
Exam 15: Multiple Regression109 Questions
Exam 16: Regression Analysis: Model Building82 Questions
Exam 17: Time Series Analysis and Forecasting80 Questions
Exam 18: Nonparametric Methods83 Questions
Exam 19: Statistical Methods for Quality Control75 Questions
Exam 20: Decision Analysis71 Questions
Exam 21: Sample Survey68 Questions
Select questions type
The degrees of freedom associated with a t distribution are a function of the
(Multiple Choice)
4.8/5  (36)
(36)
Exhibit 8-1
In order to estimate the average time spent on the computer terminals per student at a local university, data were collected from a sample of 81 business students over a one-week period. Assume the population standard deviation is 1.2 hours.
-Refer to Exhibit 8-1. With a 0.95 probability, the margin of error is approximately
(Multiple Choice)
4.8/5  (32)
(32)
Exhibit 8-1
In order to estimate the average time spent on the computer terminals per student at a local university, data were collected from a sample of 81 business students over a one-week period. Assume the population standard deviation is 1.2 hours.
-Refer to Exhibit 8-1. The standard error of the mean is
(Multiple Choice)
4.8/5  (28)
(28)
The Highway Safety Department wants to study the driving habits of individuals. A sample of 41 cars traveling on the highway revealed an average speed of 60 miles per hour and a standard deviation of 7 miles per hour. The population of car speeds is approximately normally distributed. Determine a 90% confidence interval estimate for the speed of all cars.
(Short Answer)
4.9/5  (33)
(33)
From a population that is not normally distributed and whose standard deviation is not known, a sample of 50 items is selected to develop an interval estimate for . Which of the following statements is true?
(Multiple Choice)
4.9/5  (39)
(39)
If an interval estimate is said to be constructed at the 90% confidence level, the confidence coefficient would be
(Multiple Choice)
4.8/5  (37)
(37)
A random sample of 36 students at a community college showed an average age of 25 years. Assume the ages of all students at the college are normally distributed with a standard deviation of 1.8 years. The 98% confidence interval for the average age of all students at this college is
(Multiple Choice)
4.7/5  (39)
(39)
A random sample of 100 credit sales in a department store showed an average sale of $120.00. From past data, it is known that the standard deviation of the population is $40.00.
a.Determine the standard error of the mean.
b.With a 0.95 probability, determine the margin of error.
c.What is the 95% confidence interval of the population mean?
(Short Answer)
4.7/5  (41)
(41)
A random sample of 144 observations has a mean of 20, a median of 21, and a mode of 22. The population standard deviation is known to equal 4.8. The 95.44% confidence interval for the population mean is
(Multiple Choice)
4.9/5  (36)
(36)
A random sample of 81 students at a local university showed that they work an average of 100 hours per month. The population standard deviation is known to be 27 hours. Compute a 95% confidence interval for the mean hours per month all students at the university work.
(Short Answer)
4.8/5  (41)
(41)
A simple random sample of 25 items from a normally distributed population resulted in a sample mean of 28 and a standard deviation of 7.5. Construct a 95% confidence interval for the population mean.
(Short Answer)
4.9/5  (39)
(39)
The makers of a soft drink want to identify the average age of its consumers. A sample of 16 consumers is taken. The average age in the sample was 22.5 years with a standard deviation of 5 years. Assume the population of consumer ages is normally distributed.
a.Construct a 95% confidence interval for the average age of all the consumers.
b.Construct an 80% confidence interval for the average age of all the consumers.
c.Discuss why the 95% and 80% confidence intervals are different.
(Essay)
4.8/5  (42)
(42)
A marketing firm is developing a new television advertisement for a large discount retail chain. A sample of 30 people is shown two potential ads and asked their preference. The results for ad #1 follow. Use Excel to develop a 95% confidence interval estimate of the proportion of people in the population who will prefer ad #1. 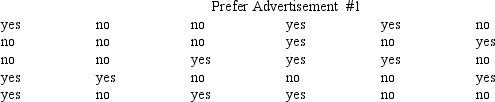
(Essay)
4.8/5  (43)
(43)
A manufacturer wants to estimate the proportion of defective items that are produced by a certain machine. A random sample of 50 items is taken. Which Excel function would not be appropriate to construct a confidence interval estimate?
(Multiple Choice)
4.7/5  (36)
(36)
A local hotel wants to estimate the proportion of its guests that are from out-of-state. Preliminary estimates are that 45% of the hotel guests are from out-of-state. How large a sample should be taken to estimate the proportion of out-of-state guests with a margin of error no larger than 5% and with a 95% level of confidence?
(Short Answer)
4.7/5  (44)
(44)
Exhibit 8-2
The manager of a grocery store has taken a random sample of 100 customers. The average length of time it took these 100 customers to check out was 3.0 minutes. It is known that the standard deviation of the checkout time is one minute.
-Refer to Exhibit 8-2. With a .95 probability, the sample mean will provide a margin of error of
(Multiple Choice)
4.9/5  (38)
(38)
A coal company wants to determine a 95% confidence interval estimate for the average daily tonnage of coal that they mine. Assuming that the company reports that the standard deviation of daily output is 200 tons, how many days should they sample so that the margin of error will be 39.2 tons or less?
(Short Answer)
4.7/5  (33)
(33)
Showing 101 - 118 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)