Exam 12: Tests of Goodness of Fit, Independence and Multiple Proportions
Exam 1: Data and Statistics85 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays112 Questions
Exam 3: Descriptive Statistics: Numerical Measures139 Questions
Exam 4: Introduction to Probability129 Questions
Exam 5: Discrete Probability Distributions150 Questions
Exam 6: Continuous Probability Distributions144 Questions
Exam 7: Sampling and Sampling Distributions119 Questions
Exam 8: Interval Estimation118 Questions
Exam 9: Hypothesis Tests118 Questions
Exam 10: Inference About Means and Proportions With Two Populations127 Questions
Exam 11: Inferences About Population Variances113 Questions
Exam 12: Tests of Goodness of Fit, Independence and Multiple Proportions76 Questions
Exam 13: Experimental Design and Analysis of Variance125 Questions
Exam 14: Simple Linear Regression103 Questions
Exam 15: Multiple Regression109 Questions
Exam 16: Regression Analysis: Model Building82 Questions
Exam 17: Time Series Analysis and Forecasting80 Questions
Exam 18: Nonparametric Methods83 Questions
Exam 19: Statistical Methods for Quality Control75 Questions
Exam 20: Decision Analysis71 Questions
Exam 21: Sample Survey68 Questions
Select questions type
Exhibit 12-6
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal. 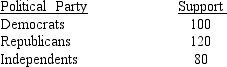 We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-The test statistic for goodness of fit has a chi-square distribution with k - 1 degrees of freedom provided that the expected frequencies for all categories are
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-The test statistic for goodness of fit has a chi-square distribution with k - 1 degrees of freedom provided that the expected frequencies for all categories are
(Multiple Choice)
4.8/5  (33)
(33)
Exhibit 12-4
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
-Refer to Exhibit 12-4. The hypothesis is to be tested at the 5% level of significance. The critical value from the table equals
(Multiple Choice)
4.8/5  (31)
(31)
Exhibit 12-3
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.  We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 12-3. The number of degrees of freedom associated with this problem is
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 12-3. The number of degrees of freedom associated with this problem is
(Multiple Choice)
5.0/5  (32)
(32)
Exhibit 12-6
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal. 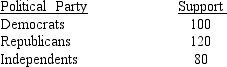 We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-A medical journal reported the following frequencies of deaths due to cardiac arrest for each day of the week:
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-A medical journal reported the following frequencies of deaths due to cardiac arrest for each day of the week:  At a 5% level of significance, determine whether the number of deaths is uniform over the week.
At a 5% level of significance, determine whether the number of deaths is uniform over the week.
(Essay)
4.9/5  (41)
(41)
Prior to the start of the season, it was expected that audience proportions for the four major news networks would be CBS 28%, NBC 35%, ABC 22% and BBC 15%. A recent sample of homes yielded the following viewing audience data.  We want to determine whether or not the recent sample supports the expectations of the number of homes of the viewing audience of the four networks.
a.State the null and alternative hypotheses to be tested.
b.Compute the test statistic.
c.The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test.
d.What do you conclude?
We want to determine whether or not the recent sample supports the expectations of the number of homes of the viewing audience of the four networks.
a.State the null and alternative hypotheses to be tested.
b.Compute the test statistic.
c.The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test.
d.What do you conclude?
(Essay)
4.8/5  (30)
(30)
Prior to the start of the season, it was expected that audience proportions for the four major news networks would be CBS 18.6%, NBC 12.5%, ABC 28.9% and BBC 40%. A recent sample of homes yielded the following viewing audience data. 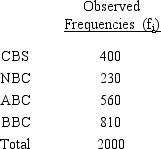 We want to determine whether or not the recent sample supports the expectations of the number of homes of the viewing audience of the four networks.
a.State the null and alternative hypotheses to be tested.
b.Compute the test statistic.
c.The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test.
d.What do you conclude?
We want to determine whether or not the recent sample supports the expectations of the number of homes of the viewing audience of the four networks.
a.State the null and alternative hypotheses to be tested.
b.Compute the test statistic.
c.The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test.
d.What do you conclude?
(Essay)
4.9/5  (25)
(25)
Exhibit 12-6
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal. 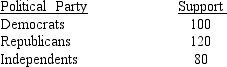 We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-Refer to Exhibit 12-6. The number of degrees of freedom associated with this problem is
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-Refer to Exhibit 12-6. The number of degrees of freedom associated with this problem is
(Multiple Choice)
4.7/5  (40)
(40)
Exhibit 12-3
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.  We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 12-3. The null hypothesis
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 12-3. The null hypothesis
(Multiple Choice)
4.9/5  (35)
(35)
City planners are evaluating three proposed alternatives for relieving the growing traffic congestion on a north-south highway in a booming city. The proposed alternatives are: (1) designate high-occupancy vehicle (HOV) lanes on the existing highway, (2) construct a new, parallel highway, and (3) construct a light (passenger) rail system.In an analysis of the three proposals, a citizen group has raised the question of whether preferences for the three alternatives differ among residents near the highway and non-residents. A test of independence will address this question, with the hypotheses being:
H0: Proposal preference is independent of the residency status of the individual
Ha: Proposal preference is not independent of the residency status of the individual
A simple random sample of 500 individuals has been selected. A crosstabulation of the residency statuses and proposal preferences of the individuals sampled is shown below.  Conduct a test of independence using = .05 to address the question of whether residency status is independent of the proposal preference.
Conduct a test of independence using = .05 to address the question of whether residency status is independent of the proposal preference.
(Essay)
4.8/5  (31)
(31)
Exhibit 12-2
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.  We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 12-2. The null hypothesis
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 12-2. The null hypothesis
(Multiple Choice)
4.7/5  (33)
(33)
Exhibit 12-4
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
-Refer to Exhibit 12-4. The conclusion of the test is that the
(Multiple Choice)
5.0/5  (44)
(44)
Shown below is a 3 * 2 contingency table with observed values from a sample of 1,500. At 95% confidence, test for independence of the row and column factors. 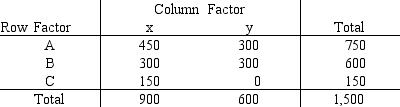
(Short Answer)
4.9/5  (46)
(46)
Exhibit 12-6
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal. 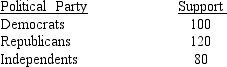 We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-The test for goodness of fit
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-The test for goodness of fit
(Multiple Choice)
4.8/5  (31)
(31)
Exhibit 12-6
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal. 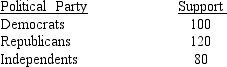 We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-Refer to Exhibit 12-6. The calculated value for the test statistic equals
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-Refer to Exhibit 12-6. The calculated value for the test statistic equals
(Multiple Choice)
4.8/5  (30)
(30)
Exhibit 12-6
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal. 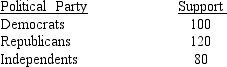 We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-In 2012, forty percent of the students at a major university were Business majors, 35% were Engineering majors and the rest of the students were majoring in other fields. In a sample of 600 students from the same university taken in 2013, two hundred were Business majors, 220 were Engineering majors and the remaining students in the sample were majoring in other fields. At a 5% significance level, test to see if there has been a significant change in the proportions between 2012 and 2013.
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-In 2012, forty percent of the students at a major university were Business majors, 35% were Engineering majors and the rest of the students were majoring in other fields. In a sample of 600 students from the same university taken in 2013, two hundred were Business majors, 220 were Engineering majors and the remaining students in the sample were majoring in other fields. At a 5% significance level, test to see if there has been a significant change in the proportions between 2012 and 2013.
(Essay)
4.9/5  (28)
(28)
Exhibit 12-6
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal. 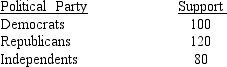 We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-A major automobile manufacturer claimed that the frequencies of repairs on all five models of its cars are the same. A sample of 200 repair services showed the following frequencies on the various makes of cars.
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-A major automobile manufacturer claimed that the frequencies of repairs on all five models of its cars are the same. A sample of 200 repair services showed the following frequencies on the various makes of cars. 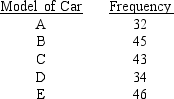 At = 0.05, test the manufacturer's claim.
At = 0.05, test the manufacturer's claim.
(Short Answer)
4.8/5  (35)
(35)
Exhibit 12-2
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.  We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 12-2. The hypothesis is to be tested at the 5% level of significance. The critical value from the table equals
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 12-2. The hypothesis is to be tested at the 5% level of significance. The critical value from the table equals
(Multiple Choice)
4.8/5  (27)
(27)
The degrees of freedom for a contingency table with 6 rows and 3 columns is
(Multiple Choice)
4.8/5  (32)
(32)
From a poll of 800 television viewers, the following data have been accumulated as to their levels of education and their preference of television stations:  Test at = .05 to determine if the selection of a TV station is dependent upon the level of education.
Test at = .05 to determine if the selection of a TV station is dependent upon the level of education.
(Essay)
4.8/5  (47)
(47)
Showing 41 - 60 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)