Exam 46: Linear Programming
Exam 1: Rectangular Coordinates69 Questions
Exam 2: Graphs of Equations63 Questions
Exam 3: Linear Equations in Two Variables61 Questions
Exam 4: Functions53 Questions
Exam 5: Analyzing Graphs of Functions56 Questions
Exam 6: A Library of Parent Functions50 Questions
Exam 7: Transformations of Functions32 Questions
Exam 8: Combinations of Functions Composite Functions58 Questions
Exam 9: Inverse Functions59 Questions
Exam 10: Mathematical Modeling and Variation49 Questions
Exam 11: Quadratic Functions and Models61 Questions
Exam 12: Polynomial Functions of Higher Degree63 Questions
Exam 13: Polynomial and Synthetic Division76 Questions
Exam 14: Complex Numbers59 Questions
Exam 15: Zeros of Polynomial Functions49 Questions
Exam 16: Rational Functions96 Questions
Exam 17: Nonlinear Inequalities56 Questions
Exam 18: Exponential Functions and Their Graphs59 Questions
Exam 19: Logarithmic Functions and Their Graphs64 Questions
Exam 20: Properties of Logarithms57 Questions
Exam 21: Exponential and Logarithmic Equations51 Questions
Exam 22: Exponential and Logarithmic Models56 Questions
Exam 23: Radian and Degree Measure52 Questions
Exam 24: Trigonometric Functions The Unit Circle50 Questions
Exam 25: Right Triangle Trigonometry56 Questions
Exam 26: Trigonometric Functions of Any Angle53 Questions
Exam 27: Graphs of Sine and Cosine Functions37 Questions
Exam 28: Graphs of Other Trigonometric Functions51 Questions
Exam 29: Inverse Trigonometric Functions50 Questions
Exam 30: Applications and Models52 Questions
Exam 31: Using Fundamental Identities60 Questions
Exam 32: Verifying Trigonometric Equations46 Questions
Exam 33: Solving Trigonometric Equations54 Questions
Exam 34: Sum and Difference Formulas62 Questions
Exam 35: Multiple Angle and Product to Sum Formulas50 Questions
Exam 36: Law of Sines43 Questions
Exam 37:Law of Cosines43 Questions
Exam 38:Vectors in the Plane50 Questions
Exam 39:Vectors and Dot Products67 Questions
Exam 40: Trigonometric Form of a Complex Number104 Questions
Exam 41: Linear and Nonlinear Systems of Equations58 Questions
Exam 42: Two Variable Linear Systems49 Questions
Exam 43: Multivariable Linear Systems54 Questions
Exam 44: Partial Fractions48 Questions
Exam 45: Systems of Inequalities50 Questions
Exam 46: Linear Programming50 Questions
Exam 47: Matrices and Systems of Equations65 Questions
Exam 48: Operations With Matrices59 Questions
Exam 49: The Inverse of a Square Matrix59 Questions
Exam 50: The Determinant of a Square Matrix52 Questions
Exam 51: Applications of Matrices and Determinants54 Questions
Exam 52: Sequences and Series68 Questions
Exam 53: Arithmetic Sequences and Partial Sums52 Questions
Exam 54: Geometric Sequences and Series67 Questions
Exam 55: Mathematical Induction48 Questions
Exam 56: The Binomial Theorem67 Questions
Exam 57: Counting Principles55 Questions
Exam 58: Probability47 Questions
Exam 59: Lines50 Questions
Exam 60: Introduction to Conics Parabolas124 Questions
Exam 61: Ellipses68 Questions
Exam 62: Hyperbolas62 Questions
Exam 63: Rotation of Conics52 Questions
Exam 64: Parametric Equations50 Questions
Exam 65: Polar Coordinates50 Questions
Exam 66: Polar Equations of Conics50 Questions
Exam 67: Graphs of Polar Equations49 Questions
Select questions type
Find the minimum value of the objective function and where it occurs,subject to the constraints:
Objective function:
Z = 4x + y
Constraints:
X ≥ 0
Y ≥ 0
3x + y ≤ 15
4x + 3y ≤ 30
(Multiple Choice)
4.8/5  (32)
(32)
An accounting firm has 780 hours of staff time and 272 hours of reviewing time available each week.The firm charges $1700 for an audit and $410 for a tax return.Each audit requires 60 hours of staff time and 16 hours of review time.Each tax return requires 10 hours of staff time and 4 hours of review time.What numbers of audits and tax returns will yield an optimal revenue? What is the optimal revenue?
(Multiple Choice)
4.8/5  (34)
(34)
Find the minimum value of the objective function and where it occurs,subject to the constraints: ?
Objective function:
?
Z = 8x + y
?
Constraints:
?
X ? 0
Y ? 0
X + 4y ? 20
X + y ? 18
?2x + 2y ? 21
?
(Multiple Choice)
4.9/5  (38)
(38)
Select the region determined by the constraints.Then find the maximum value of the objective function (if possible)and where it occurs,subject to the indicated constraints.
Objective function:
Z = 3x + 2y
Constraints:
X ≥ 0
y ≥ 0
5x + 2y ≤ 20
5x + y ≥ 10
(Multiple Choice)
4.8/5  (33)
(33)
The linear programming problem has an unusual characteristic.Select a graph of the solution region for the problem and describe the unusual characteristic.Find the maximum value of the objective function (if possible)and where it occurs.
Objective function:
Z = -x + 3y
Constraints:
X ≥ 0
Y ≥ 0
X ≤ 10
X + y ≤ 7
(Multiple Choice)
4.8/5  (47)
(47)
A manufacturer produces two models of elliptical cross-training exercise machines. The times for assembling,finishing,and packaging model X are 3 hours,3 hours,and 0.8 hour,respectively.The times for model Y are 4 hours,2.5 hours,and 0.4 hour.The total times available for assembling,finishing,and packaging are 6000 hours,4200 hours,and 950 hours,respectively.The profits per unit are $200 for model X and $275 for model Y.What is the optimal production level for each model? What is the optimal profit?
(Multiple Choice)
4.7/5  (46)
(46)
The linear programming problem has an unusual characteristic.Select a graph of the solution region for the problem and describe the unusual characteristic.Find the minimum and maximum value of the objective function (if possible)and where it occurs.
Z = x + y
Constraints:
X ≥ 0
Y ≥ 0
-x + y ≤ 0
-5x + y ≥ 5
(Multiple Choice)
4.8/5  (40)
(40)
According to automobile association of a country,on March 27,2009,the national average price per gallon of regular unleaded (87-octane)gasoline was $2.07,and the price of premium unleaded (90-octane)gasoline was $2.25.Write an objective function that models the cost of the blend of mid-grade unleaded gasoline (89-octane).
(Multiple Choice)
4.9/5  (24)
(24)
The linear programming problem has an unusual characteristic.Select a graph of the solution region for the problem and describe the unusual characteristic.Find the maximum value of the objective function (if possible)and where it occurs.
Objective function:
Z = x + y
Constraints:
X ≥ 0
Y ≥ 0
-x + y ≤ 1
-x + 5y ≤ 7
(Multiple Choice)
4.9/5  (45)
(45)
Find the minimum value of the objective function and where it occurs,subject to the indicated constraints.
Objective function:
Z = 4x + 5y
Constraints:
X ≥ 0
3x - y ≤ 9
2x + 3y ≥ 6
X + 4y ≤ 16
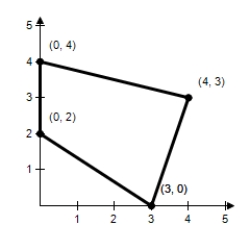
(Multiple Choice)
4.7/5  (32)
(32)
Showing 41 - 50 of 50
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)