Exam 10: Mathematical Modeling and Variation
Exam 1: Rectangular Coordinates69 Questions
Exam 2: Graphs of Equations63 Questions
Exam 3: Linear Equations in Two Variables61 Questions
Exam 4: Functions53 Questions
Exam 5: Analyzing Graphs of Functions56 Questions
Exam 6: A Library of Parent Functions50 Questions
Exam 7: Transformations of Functions32 Questions
Exam 8: Combinations of Functions Composite Functions58 Questions
Exam 9: Inverse Functions59 Questions
Exam 10: Mathematical Modeling and Variation49 Questions
Exam 11: Quadratic Functions and Models61 Questions
Exam 12: Polynomial Functions of Higher Degree63 Questions
Exam 13: Polynomial and Synthetic Division76 Questions
Exam 14: Complex Numbers59 Questions
Exam 15: Zeros of Polynomial Functions49 Questions
Exam 16: Rational Functions96 Questions
Exam 17: Nonlinear Inequalities56 Questions
Exam 18: Exponential Functions and Their Graphs59 Questions
Exam 19: Logarithmic Functions and Their Graphs64 Questions
Exam 20: Properties of Logarithms57 Questions
Exam 21: Exponential and Logarithmic Equations51 Questions
Exam 22: Exponential and Logarithmic Models56 Questions
Exam 23: Radian and Degree Measure52 Questions
Exam 24: Trigonometric Functions The Unit Circle50 Questions
Exam 25: Right Triangle Trigonometry56 Questions
Exam 26: Trigonometric Functions of Any Angle53 Questions
Exam 27: Graphs of Sine and Cosine Functions37 Questions
Exam 28: Graphs of Other Trigonometric Functions51 Questions
Exam 29: Inverse Trigonometric Functions50 Questions
Exam 30: Applications and Models52 Questions
Exam 31: Using Fundamental Identities60 Questions
Exam 32: Verifying Trigonometric Equations46 Questions
Exam 33: Solving Trigonometric Equations54 Questions
Exam 34: Sum and Difference Formulas62 Questions
Exam 35: Multiple Angle and Product to Sum Formulas50 Questions
Exam 36: Law of Sines43 Questions
Exam 37:Law of Cosines43 Questions
Exam 38:Vectors in the Plane50 Questions
Exam 39:Vectors and Dot Products67 Questions
Exam 40: Trigonometric Form of a Complex Number104 Questions
Exam 41: Linear and Nonlinear Systems of Equations58 Questions
Exam 42: Two Variable Linear Systems49 Questions
Exam 43: Multivariable Linear Systems54 Questions
Exam 44: Partial Fractions48 Questions
Exam 45: Systems of Inequalities50 Questions
Exam 46: Linear Programming50 Questions
Exam 47: Matrices and Systems of Equations65 Questions
Exam 48: Operations With Matrices59 Questions
Exam 49: The Inverse of a Square Matrix59 Questions
Exam 50: The Determinant of a Square Matrix52 Questions
Exam 51: Applications of Matrices and Determinants54 Questions
Exam 52: Sequences and Series68 Questions
Exam 53: Arithmetic Sequences and Partial Sums52 Questions
Exam 54: Geometric Sequences and Series67 Questions
Exam 55: Mathematical Induction48 Questions
Exam 56: The Binomial Theorem67 Questions
Exam 57: Counting Principles55 Questions
Exam 58: Probability47 Questions
Exam 59: Lines50 Questions
Exam 60: Introduction to Conics Parabolas124 Questions
Exam 61: Ellipses68 Questions
Exam 62: Hyperbolas62 Questions
Exam 63: Rotation of Conics52 Questions
Exam 64: Parametric Equations50 Questions
Exam 65: Polar Coordinates50 Questions
Exam 66: Polar Equations of Conics50 Questions
Exam 67: Graphs of Polar Equations49 Questions
Select questions type
State sales tax is based on retail price.An item that sells for $180.99 has a sales tax of $17.4.Find a mathematical model that gives the amount of sales tax y in terms of the retail price x.Use the model to find the sales tax on a $589.99 purchase.(Round your answer to four decimal places. )
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
B
An overhead garage door has two springs,one on each side of the door (see figure).A force of pounds is required to stretch each spring 1 foot.Because of a pulley system,the springs stretch only one-half the distance the door travels.The door moves a total of feet,and the springs are at their natural length when the door is open.Find the combined lifting force applied to the door by the springs when the door is closed. 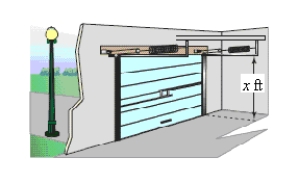
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
B
Use the given value of k to complete the table for the direct variation model .
Plot the points on a rectangular coordinate system.
x 8 10 12 14 16 y=k k=
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
A
Use the given value of k to complete the table for the inverse variation model Plot the points on a rectangular coordinate system. x 8 10 12 14 16 y= k=5
(Multiple Choice)
4.8/5  (31)
(31)
On a yardstick with scales in inches and centimeters,you notice that 11 inches is approximately the same length as 33 centimeters.Use this information to find a mathematical model that relates centimeters y to inches x.Then use the model to find the numbers of centimeters in 60 inches and 70 inches.(Round your answer to one decimal place. )
(Multiple Choice)
4.7/5  (39)
(39)
Assume that y is directly proportional to x.Use the given x-value and y-value to find a linear model that relates y and x.
(Multiple Choice)
4.8/5  (38)
(38)
Determine whether the variation model below is of the form or . x
12
24
36
48
60
Y
(Multiple Choice)
4.8/5  (40)
(40)
Find a mathematical model representing the statement.(Determine the constant of proportionality. )
F is jointly proportional to r and the third power of s.
(Multiple Choice)
4.9/5  (42)
(42)
Determine whether the variation model is of the form or and find k.Then write a model that relates y and x. x 5 10 15 20 25 y -1.5 -3 -4.5 -6 -7.5
(Multiple Choice)
4.8/5  (31)
(31)
Determine whether the variation model below is of the form or . x
13
26
39
52
65
Y
3
6
9
12
15
(Multiple Choice)
4.9/5  (29)
(29)
Find a mathematical model for the verbal statement: "m varies directly as the square of w and inversely as s."
(Multiple Choice)
4.8/5  (37)
(37)
Find a mathematical model representing the statement.(Determine the constant of proportionality. )
Y varies inversely as x.
(Multiple Choice)
4.9/5  (34)
(34)
Assume that y is directly proportional to x.Use the given x-value and y-value to find a linear model that relates y and x.
(Multiple Choice)
4.9/5  (35)
(35)
The coiled spring of a toy supports the weight of a child.The spring is compressed a distance of 1.6 inches by the weight of a 35-pound child.The toy will not work properly if its spring is compressed more than 6 inches.What is the weight of the heaviest child who should be allowed to use the toy? (Round your answer to two decimal places. )
(Multiple Choice)
4.9/5  (21)
(21)
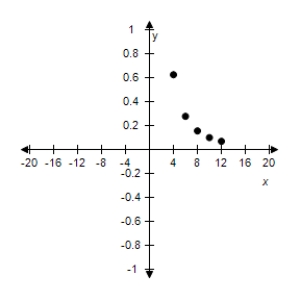
Use the given value of k to complete the table for the inverse variation model Plot the points on a rectangular coordinate system.
x 8 10 12 14 16 y=
(Multiple Choice)
4.8/5  (35)
(35)
When buying gasoline,you notice that 16 gallons of gasoline is approximately the same amount of gasoline as 51 liters.Use this information to find a linear model that relates liters y to gallons x.Then use the model to find the numbers of liters in 25 gallons and 45 gallons. (Round your answer to one decimal place. )
(Multiple Choice)
4.8/5  (39)
(39)
The sales tax on an item with a retail price of $972 is $68.04.Create a variational model that gives the retail price,y,in terms of the sales tax,x,and use it to determine the retail price of an item that has a sales tax of $82.62.
(Multiple Choice)
4.7/5  (30)
(30)
Use the fact that the diameter of the largest particle that can be moved by a stream varies approximately directly as the square of the velocity of the stream.
A stream with a velocity of mile per hour can move coarse sand particles about 0.07 inch in diameter.Approximate the velocity required to carry particles 0.2 inch in diameter.(Round your answer to two decimal places. )
(Multiple Choice)
4.8/5  (36)
(36)
Find a mathematical model for the verbal statement:
"Q is jointly proportional to the cube of h and the square root of m."
(Multiple Choice)
4.8/5  (37)
(37)
Use the given value of k to complete the table for the direct variation model .
Plot the points on a rectangular coordinate system.
x 8 10 12 14 16 y=k k=
(Multiple Choice)
4.8/5  (28)
(28)
Showing 1 - 20 of 49
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)