Exam 31: Using Fundamental Identities
Exam 1: Rectangular Coordinates69 Questions
Exam 2: Graphs of Equations63 Questions
Exam 3: Linear Equations in Two Variables61 Questions
Exam 4: Functions53 Questions
Exam 5: Analyzing Graphs of Functions56 Questions
Exam 6: A Library of Parent Functions50 Questions
Exam 7: Transformations of Functions32 Questions
Exam 8: Combinations of Functions Composite Functions58 Questions
Exam 9: Inverse Functions59 Questions
Exam 10: Mathematical Modeling and Variation49 Questions
Exam 11: Quadratic Functions and Models61 Questions
Exam 12: Polynomial Functions of Higher Degree63 Questions
Exam 13: Polynomial and Synthetic Division76 Questions
Exam 14: Complex Numbers59 Questions
Exam 15: Zeros of Polynomial Functions49 Questions
Exam 16: Rational Functions96 Questions
Exam 17: Nonlinear Inequalities56 Questions
Exam 18: Exponential Functions and Their Graphs59 Questions
Exam 19: Logarithmic Functions and Their Graphs64 Questions
Exam 20: Properties of Logarithms57 Questions
Exam 21: Exponential and Logarithmic Equations51 Questions
Exam 22: Exponential and Logarithmic Models56 Questions
Exam 23: Radian and Degree Measure52 Questions
Exam 24: Trigonometric Functions The Unit Circle50 Questions
Exam 25: Right Triangle Trigonometry56 Questions
Exam 26: Trigonometric Functions of Any Angle53 Questions
Exam 27: Graphs of Sine and Cosine Functions37 Questions
Exam 28: Graphs of Other Trigonometric Functions51 Questions
Exam 29: Inverse Trigonometric Functions50 Questions
Exam 30: Applications and Models52 Questions
Exam 31: Using Fundamental Identities60 Questions
Exam 32: Verifying Trigonometric Equations46 Questions
Exam 33: Solving Trigonometric Equations54 Questions
Exam 34: Sum and Difference Formulas62 Questions
Exam 35: Multiple Angle and Product to Sum Formulas50 Questions
Exam 36: Law of Sines43 Questions
Exam 37:Law of Cosines43 Questions
Exam 38:Vectors in the Plane50 Questions
Exam 39:Vectors and Dot Products67 Questions
Exam 40: Trigonometric Form of a Complex Number104 Questions
Exam 41: Linear and Nonlinear Systems of Equations58 Questions
Exam 42: Two Variable Linear Systems49 Questions
Exam 43: Multivariable Linear Systems54 Questions
Exam 44: Partial Fractions48 Questions
Exam 45: Systems of Inequalities50 Questions
Exam 46: Linear Programming50 Questions
Exam 47: Matrices and Systems of Equations65 Questions
Exam 48: Operations With Matrices59 Questions
Exam 49: The Inverse of a Square Matrix59 Questions
Exam 50: The Determinant of a Square Matrix52 Questions
Exam 51: Applications of Matrices and Determinants54 Questions
Exam 52: Sequences and Series68 Questions
Exam 53: Arithmetic Sequences and Partial Sums52 Questions
Exam 54: Geometric Sequences and Series67 Questions
Exam 55: Mathematical Induction48 Questions
Exam 56: The Binomial Theorem67 Questions
Exam 57: Counting Principles55 Questions
Exam 58: Probability47 Questions
Exam 59: Lines50 Questions
Exam 60: Introduction to Conics Parabolas124 Questions
Exam 61: Ellipses68 Questions
Exam 62: Hyperbolas62 Questions
Exam 63: Rotation of Conics52 Questions
Exam 64: Parametric Equations50 Questions
Exam 65: Polar Coordinates50 Questions
Exam 66: Polar Equations of Conics50 Questions
Exam 67: Graphs of Polar Equations49 Questions
Select questions type
By using a graphing utility to complete the following table.Round your answer to four decimal places. x 0.8 1.0 1.2 1.4 1.6 1.8 2.0 \@cdots \@cdots \@cdots \@cdots \@cdots \@cdots \@cdots \ldots \ldots \ldots \ldots \ldots \ldots \@cdots
Free
(Multiple Choice)
4.9/5  (42)
(42)
Correct Answer:
E
Use the trigonometric substitution to rewrite the algebraic expression as a trigonometric function of θ,where .
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
B
Find the rate of change of the function .
Free
(Multiple Choice)
4.7/5  (38)
(38)
Correct Answer:
E
Which of the following is equivalent to the given expression?
(Multiple Choice)
4.9/5  (28)
(28)
Factor;then use fundamental identities to simplify the expression below and determine which of the following is not equivalent.
(Multiple Choice)
4.8/5  (42)
(42)
Use the trigonometric substitution to rewrite the algebraic expression as a trigonometric function of θ,where .Then find sin θ and cos θ.
(Multiple Choice)
4.9/5  (31)
(31)
Rewrite as a single logarithm and then simplify the result.
(Multiple Choice)
4.9/5  (33)
(33)
Use the given values to evaluate (if possible)three trigonometric functions sin x,cos x,cot x.
(Multiple Choice)
4.9/5  (27)
(27)
If x = 2 tan θ,use trigonometric substitution to write as a trigonometric function of θ,where .
(Multiple Choice)
4.8/5  (34)
(34)
If x = 2 tan θ,use trigonometric substitution to write as a trigonometric function of θ,where .
(Multiple Choice)
4.7/5  (27)
(27)
Use a graphing utility to determine which of the trigonometric functions is equal to the following expression.
(Multiple Choice)
4.7/5  (33)
(33)
Use the trigonometric substitution to rewrite the algebraic expression as a trigonometric function of θ,where .
(Multiple Choice)
4.9/5  (32)
(32)
The forces acting on an object weighing W units on an inclined plane positioned at an angle of θ with the horizontal (see figure)are modeled by where μ is the coefficient of friction.Solve the equation for μ and simplify the result. 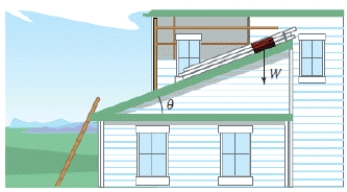
(Multiple Choice)
4.8/5  (26)
(26)
Factor;then use fundamental identities to simplify the expression below and determine which of the following is not equivalent.
(Multiple Choice)
4.8/5  (36)
(36)
Factor;then use fundamental identities to simplify the expression below and determine which of the following is not equivalent.
(Multiple Choice)
4.8/5  (32)
(32)
By using a graphing utility to complete the following table.Round your answer to two decimal places. x 0.2 0.4 0.6 0.8 1 1.2 1.4 - - - - - - - - - - - - - -
(Multiple Choice)
4.9/5  (43)
(43)
Use the fundamental identities to simplify the expression.
Cot θ sec θ
(Multiple Choice)
4.8/5  (39)
(39)
Use fundamental identities to simplify the expression below and then determine which of the following is not equivalent.
(Multiple Choice)
4.9/5  (36)
(36)
Use the given values to evaluate (if possible)three trigonometric functions cos x,csc x,tan x.
(Multiple Choice)
4.8/5  (38)
(38)
Showing 1 - 20 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)