Exam 60: Introduction to Conics Parabolas
Exam 1: Rectangular Coordinates69 Questions
Exam 2: Graphs of Equations63 Questions
Exam 3: Linear Equations in Two Variables61 Questions
Exam 4: Functions53 Questions
Exam 5: Analyzing Graphs of Functions56 Questions
Exam 6: A Library of Parent Functions50 Questions
Exam 7: Transformations of Functions32 Questions
Exam 8: Combinations of Functions Composite Functions58 Questions
Exam 9: Inverse Functions59 Questions
Exam 10: Mathematical Modeling and Variation49 Questions
Exam 11: Quadratic Functions and Models61 Questions
Exam 12: Polynomial Functions of Higher Degree63 Questions
Exam 13: Polynomial and Synthetic Division76 Questions
Exam 14: Complex Numbers59 Questions
Exam 15: Zeros of Polynomial Functions49 Questions
Exam 16: Rational Functions96 Questions
Exam 17: Nonlinear Inequalities56 Questions
Exam 18: Exponential Functions and Their Graphs59 Questions
Exam 19: Logarithmic Functions and Their Graphs64 Questions
Exam 20: Properties of Logarithms57 Questions
Exam 21: Exponential and Logarithmic Equations51 Questions
Exam 22: Exponential and Logarithmic Models56 Questions
Exam 23: Radian and Degree Measure52 Questions
Exam 24: Trigonometric Functions The Unit Circle50 Questions
Exam 25: Right Triangle Trigonometry56 Questions
Exam 26: Trigonometric Functions of Any Angle53 Questions
Exam 27: Graphs of Sine and Cosine Functions37 Questions
Exam 28: Graphs of Other Trigonometric Functions51 Questions
Exam 29: Inverse Trigonometric Functions50 Questions
Exam 30: Applications and Models52 Questions
Exam 31: Using Fundamental Identities60 Questions
Exam 32: Verifying Trigonometric Equations46 Questions
Exam 33: Solving Trigonometric Equations54 Questions
Exam 34: Sum and Difference Formulas62 Questions
Exam 35: Multiple Angle and Product to Sum Formulas50 Questions
Exam 36: Law of Sines43 Questions
Exam 37:Law of Cosines43 Questions
Exam 38:Vectors in the Plane50 Questions
Exam 39:Vectors and Dot Products67 Questions
Exam 40: Trigonometric Form of a Complex Number104 Questions
Exam 41: Linear and Nonlinear Systems of Equations58 Questions
Exam 42: Two Variable Linear Systems49 Questions
Exam 43: Multivariable Linear Systems54 Questions
Exam 44: Partial Fractions48 Questions
Exam 45: Systems of Inequalities50 Questions
Exam 46: Linear Programming50 Questions
Exam 47: Matrices and Systems of Equations65 Questions
Exam 48: Operations With Matrices59 Questions
Exam 49: The Inverse of a Square Matrix59 Questions
Exam 50: The Determinant of a Square Matrix52 Questions
Exam 51: Applications of Matrices and Determinants54 Questions
Exam 52: Sequences and Series68 Questions
Exam 53: Arithmetic Sequences and Partial Sums52 Questions
Exam 54: Geometric Sequences and Series67 Questions
Exam 55: Mathematical Induction48 Questions
Exam 56: The Binomial Theorem67 Questions
Exam 57: Counting Principles55 Questions
Exam 58: Probability47 Questions
Exam 59: Lines50 Questions
Exam 60: Introduction to Conics Parabolas124 Questions
Exam 61: Ellipses68 Questions
Exam 62: Hyperbolas62 Questions
Exam 63: Rotation of Conics52 Questions
Exam 64: Parametric Equations50 Questions
Exam 65: Polar Coordinates50 Questions
Exam 66: Polar Equations of Conics50 Questions
Exam 67: Graphs of Polar Equations49 Questions
Select questions type
Find the center and vertices which located on the major axis of the ellipse from given equation and select its graph.
(Multiple Choice)
4.7/5  (41)
(41)
Find the standard form of the equation of the parabola and determine the coordinates of the focus. 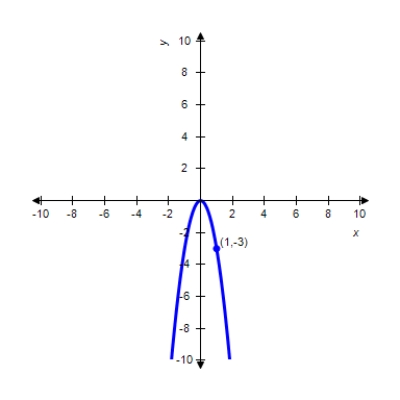
(Multiple Choice)
4.8/5  (42)
(42)
Find the standard form of the equation of the hyperbola with the given characteristics and center at the origin.
Vertices: (0,±3);focies: (0,±7)
(Multiple Choice)
4.9/5  (38)
(38)
Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. focus: (0,-1)
(Multiple Choice)
5.0/5  (35)
(35)
Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin.
Vertical axis and passes through the point (6,8)
(Multiple Choice)
4.8/5  (39)
(39)
Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin.
Vertical axis and passes through the point (-8,-8)
(Multiple Choice)
4.7/5  (32)
(32)
Find the standard form of the equation of the hyperbola with the given characteristics and center at the origin.
Vertices: (0,±5);focies: (0,±6)
(Multiple Choice)
4.9/5  (30)
(30)
Find the standard form of the equation of the parabola and determine the coordinates of the focus. 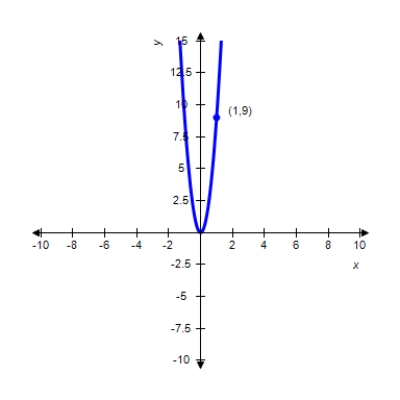
(Multiple Choice)
4.9/5  (31)
(31)
Give the coordinates of the circle's center and its radius.
Enter your answer using the coordinate notation: (a,b)and r = ....separated with a comma.
(Short Answer)
4.9/5  (30)
(30)
Sketch the graph of the ellipse,using the lateral recta.
(Multiple Choice)
4.9/5  (41)
(41)
The revenue R (in dollars)generated by the sale of x units of a patio furniture set is given by .Select the correct graph of the function.
(Multiple Choice)
4.7/5  (27)
(27)
Find the standard form of the equation of the parabola with the given characteristic(s)and vertex at the origin.
Directrix: x = -4
(Multiple Choice)
4.9/5  (36)
(36)
Find the equation of the parabola with vertex at (0,0)and focus at (0,5).
(Multiple Choice)
4.7/5  (35)
(35)
Find the standard form of the equation of the parabola with the given characteristic(s)and vertex at the origin.
Focus:
(Multiple Choice)
4.8/5  (26)
(26)
In a suspension bridge,the shape of the suspension cables is parabolic.The bridge shown in the figure has towers that are 1000 m apart,and the lowest point of the suspension cables is 200 m below the top of the towers.Find the equation of the parabolic part of the cables,placing the origin of the coordinate system at the lowest point of the cable.
NOTE: This equation is used to find the length of the cable needed in the construction of the bridge. 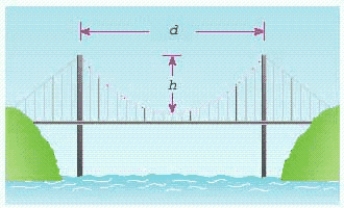
(Multiple Choice)
4.8/5  (29)
(29)
Showing 21 - 40 of 124
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)