Exam 8: Further Applications of Integration
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Let a) For what value of c is f a probability density function?
b) For that value of c, find P (-1 < X < 1).
(Short Answer)
4.8/5  (38)
(38)
A cylindrical drum of diameter 2 ft and length 6 ft is lying on its side, submerged in water 16 ft deep. Find the force exerted by the water on one end of the drum to the nearest pound. (The weight density of water is 62.4 lb/ft3.)
(Short Answer)
4.7/5  (24)
(24)
For a given commodity and pure competition, the number of units produced and the price per unit are determined as the coordinates of the point of intersection of the supply and demand curves. Given the demand curve and the supply curve ,
find the consumer surplus.
(Short Answer)
4.8/5  (48)
(48)
Find the centroid of the region bounded by the graphs of the given equations.
(Short Answer)
4.9/5  (32)
(32)
If f (x) is the probability density function for the blood cholesterol level of men over the age of 40, where x is measured in milligrams per deciliter, express as an integral the probability that the cholesterol level of such a man lies between 195 and .
(Multiple Choice)
4.8/5  (40)
(40)
Find the center of mass of the lamina of the region shown if the density of the circular lamina is five times that of the rectangular lamina. 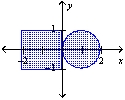
(Short Answer)
4.9/5  (48)
(48)
Find the area of the surface obtained by revolving the given curve about the x-axis. on [0, 1]
(Short Answer)
4.8/5  (30)
(30)
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is 62.4 lb/ft3.) 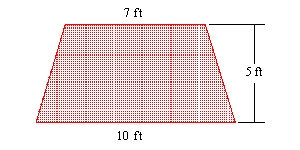
(Short Answer)
4.9/5  (34)
(34)
Find the area of the region under the graph of f on [a, b].
(Multiple Choice)
4.9/5  (32)
(32)
Boxes are labeled as containing 500 g of cereal. The machine filling the boxes produces weights that are normally distributed with standard deviation 12
G) If the target weight is 500 g, what is the probability that the machine produces a box with less than g of cereal? Round your answer to four decimal places.
(Short Answer)
4.8/5  (34)
(34)
A vertical plate is submerged in water (the surface of the water coincides with the x-axis). Find the force exerted by the water on the plate. (The weight density of water is 62.4 lb/ft3.) 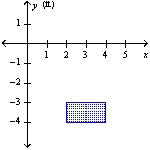 (ft)
(ft)
(Multiple Choice)
4.9/5  (41)
(41)
A gate in an irrigation canal is constructed in the form of a trapezoid ft wide at the bottom, ft wide at the top, and 2 ft high. It is placed vertically in the canal, with the water extending to its top. Find the hydrostatic force on one side of the gate..
(Multiple Choice)
4.7/5  (41)
(41)
A swimming pool is 10 ft wide and 36 ft long and its bottom is an inclined plane, the shallow end having a depth of 1 ft and the deep end, 12 ft. If the pool is full of water, find the hydrostatic force on the shallow end. (Use the fact that water weighs 62.5 lb/ .)
(Short Answer)
4.8/5  (35)
(35)
Find the centroid of the region bounded by the given curves.
(Multiple Choice)
4.9/5  (32)
(32)
Find the centroid of the region bounded by the graphs of the given equations.
(Multiple Choice)
4.8/5  (39)
(39)
For the following exercise, (a) plot the graph of the function f, (b) write an integral giving the arc length of the graph of the function over the indicated interval, and (c) find the arc length of the curve accurate to two decimal places. = x - ; [0, 6]
(Short Answer)
4.9/5  (42)
(42)
Find the center of mass of the system comprising masses mk located at the points Pk in a coordinate plane. Assume that mass is measured in grams and distance is measured in centimeters.
m1 = 3, m2 = 4, m3 = 5
P1 (-3, 5), P2 (3, 4), P3 (-4, 1)
(Short Answer)
4.9/5  (37)
(37)
Showing 21 - 40 of 87
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)