Exam 8: Further Applications of Integration
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Use the Theorem of Pappus to find the volume of the solid obtained by revolving the region bounded by the graphs of and about the y-axis.
(Multiple Choice)
4.9/5  (22)
(22)
Find the arc length of the graph of the given equation on the specified interval. y = ( + 1)
, [2, 5]
(Multiple Choice)
4.8/5  (37)
(37)
A vertical plate is submerged in water (the surface of the water coincides with the x-axis). Find the force exerted by the water on the plate. (The weight density of water is 62.4 lb/ft3.) 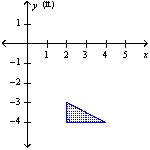 (ft)
(ft)
(Short Answer)
4.9/5  (34)
(34)
Find the centroid of the region bounded by the graphs of and .
(Short Answer)
5.0/5  (35)
(35)
Find the centroid of the region bounded by the graphs of and .
(Short Answer)
4.8/5  (37)
(37)
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is 62.4 lb/ft3.) 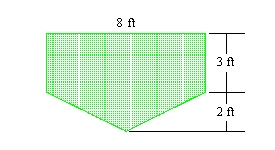
(Short Answer)
4.9/5  (39)
(39)
Showing 81 - 87 of 87
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)