Exam 8: Further Applications of Integration
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
If the infinite curve , is rotated about the x-axis , find the area of the resulting surface.
(Multiple Choice)
4.7/5  (45)
(45)
Suppose the average waiting time for a customer's call to be answered by a company representative (modeled by exponentially decreasing probability density functions) is minutes. Find the median waiting time.
(Multiple Choice)
4.8/5  (29)
(29)
Set up, but do not evaluate, an integral that represents the length of the curve.
(Short Answer)
4.9/5  (41)
(41)
Find the arc length of the graph of the given equation from P to Q.
y = - 3x + 2; P (3, -7), Q (6, -16)
(Short Answer)
4.9/5  (39)
(39)
The standard deviation for a random variable with probability density function f and mean µ is defined . Find the standard deviation for an exponential density function with mean .
(Multiple Choice)
4.7/5  (34)
(34)
Find the area of the surface obtained by revolving the given curve about the x-axis. on
(Multiple Choice)
4.8/5  (39)
(39)
Find the length of the line segment joining the two given points by finding the equation of the line using Equation (2). Then check your answer by using the distance formula. (0, 0), (1, 8)
(Multiple Choice)
4.8/5  (39)
(39)
Let the function whose graph is shown be a probability density function. Calculate the mean. 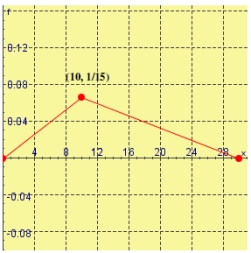
(Short Answer)
4.7/5  (36)
(36)
The marginal revenue from producing x units of a certain product is (in dollars per unit). Find the increase in revenue if the production level is raised from 1,100 units to units.
(Multiple Choice)
5.0/5  (33)
(33)
Find the area of the surface obtained by revolving the graph of y = on [0, 1] about the x-axis.
(Short Answer)
4.9/5  (32)
(32)
The masses are located at the point . Find the moments and and the center of mass of the system. ;
(Multiple Choice)
4.8/5  (35)
(35)
The manager of a fast-food restaurant determines that the average time that her customers wait for service is 2 minutes.
The manager wants to advertise that anybody who isn't served within a certain number of minutes gets a free hamburger. But she doesn't want to give away free hamburgers to more than % of her customers. What value of x must she use in the advertisement "if you aren't served within x minutes, you get a free hamburger"?
(Short Answer)
4.9/5  (31)
(31)
Find the area of the surface obtained by rotating the curve about the x-axis.
(Multiple Choice)
4.8/5  (32)
(32)
Find the volume obtained when the circle of radius 2 with center ( 2 , 0) is rotated about the y-axis.
(Multiple Choice)
4.9/5  (31)
(31)
A rectangular tank has width 4 ft, height 4 ft, and length 7 ft. It is filled with equal volumes of water and oil. The oil has a weight density of 50 lb/ft3 and floats on the water. Find the force exerted by the mixture on one end of the tank. (The weight density of water is 62.4 lb/ft3.)
(Multiple Choice)
4.8/5  (35)
(35)
Set up, but do not evaluate, an integral for the area of the surface obtained by rotating the curve about the x-axis on the interval .
(Multiple Choice)
4.9/5  (43)
(43)
Find the coordinates of the centroid for the region bounded by the curves , x = 0,
and y = 72 .
(Short Answer)
4.9/5  (30)
(30)
Find the center of mass of a lamina in the shape of a quarter-circle with radius 9 with density = 3 . 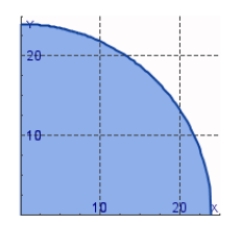
(Short Answer)
4.9/5  (36)
(36)
Showing 61 - 80 of 87
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)