Exam 6: Inverse Functions
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
The volume of a solid torus (the donut-shaped solid shown in the figure) with r = 5 and R = 15 is 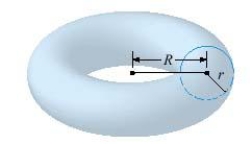
(True/False)
4.9/5  (38)
(38)
Newton's Law of Gravitation states that two bodies with masses attract each other with a force where r is the distance between the bodies and G is the gravitation constant. If one of bodies is fixed, find the work needed to move the other from to .
(Multiple Choice)
4.9/5  (34)
(34)
Find the volume of the frustum of a pyramid with square base of side square top of side and height 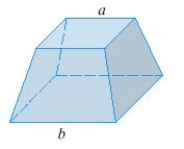
(Short Answer)
4.8/5  (34)
(34)
A bucket weighs 7 lb and a rope of negligible weight are used to draw water from a well that is 60 ft deep. The bucket starts with 50 lb of water and is pulled up at a rate of 10 ft/s, but water leaks out of a hole in the bucket at a rate of 0.5 lb/s. Find the work done in pulling the bucket to the top of the well.
(Multiple Choice)
4.8/5  (44)
(44)
The Mean Value Theorem for Integrals says that if is continuous on [ , ], then there exists a number m in [ , ] such that
(True/False)
4.7/5  (38)
(38)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. , , , ; the x-axis
(Short Answer)
4.8/5  (30)
(30)
Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis.
(Short Answer)
4.8/5  (34)
(34)
In a steam engine the pressure and volume of steam satisfy the equation , where k is a constant. (This is true for adiabatic expansion, that is, expansion in which there is no heat transfer between the cylinder and its surroundings.) Calculate the work done by the engine (in ft-lb) during a cycle when the steam starts at a pressure of and a volume of and expands to a volume of Use the fact that the work done by the gas when the volume expands from to volume is .
(Short Answer)
4.9/5  (36)
(36)
Sketch the region bounded by the graphs of the given equations and find the area of that region.
y = + 4, y = 2x + 1
(Short Answer)
4.8/5  (42)
(42)
Sketch the region bounded by the graphs of the given equations and find the area of that region. y = sec2 x + 6, y = 8, x = - , x =
(Multiple Choice)
4.9/5  (40)
(40)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations and inequalities about the y-axis. - = 16, x 0, y = - 4, y = 4
(Multiple Choice)
4.9/5  (34)
(34)
The temperature of a metal rod, 6 m long, is 5 x (in degree Celsius) at a distance x meters from one end of the rod. What is the average temperature of the rod?
(Multiple Choice)
4.8/5  (42)
(42)
Suppose you make napkin rings by drilling holes with different diameters through two wooden balls (which also have different diameters). You discover that both napkin rings have the same height h as shown in the figure. Use cylindrical shells to compute the volume of a napkin ring created by drilling a hole with radius d through the center of a sphere of radius D and express the answer in terms of . 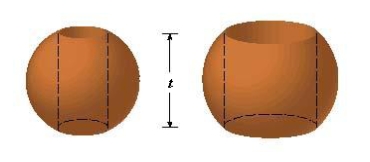
(Multiple Choice)
4.8/5  (38)
(38)
A tank is full of water. Find the work required to pump the water out of the outlet. 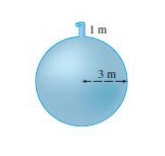
(Multiple Choice)
4.8/5  (39)
(39)
Find the volume of the solid obtained by rotating the region bounded by and about the y-axis.
(Short Answer)
4.8/5  (35)
(35)
Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis.
(Short Answer)
4.9/5  (41)
(41)
Sketch the region enclosed by . Find t he area of the region.
(Multiple Choice)
4.8/5  (47)
(47)
Showing 21 - 40 of 95
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)