Exam 6: Inverse Functions
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
A heavy rope, 40 ft long, weighs lb/ft and hangs over the edge of a building 110 ft high. How much work is done in pulling the rope to the top of the building?
(Multiple Choice)
4.8/5  (42)
(42)
Use the Midpoint Rule with n = 4 to estimate the volume obtained by rotating about the region under the y-axis the region under the curve. Select the correct answer. The choices are rounded to the nearest hundredth.
(Multiple Choice)
4.9/5  (36)
(36)
Use the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle. , y = 0, x = 1, x = 12; the y-axis
(Short Answer)
4.9/5  (42)
(42)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated line. Sketch the region and a representative rectangle.
y = , y = x - 1; the line x = 2
(Short Answer)
4.8/5  (52)
(52)
The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. Round your answer to 3 decimal places. about the y-axis and .
(Multiple Choice)
4.8/5  (39)
(39)
A spring has a natural length of 20 cm. If a force of 25 N is required to keep it stretched to a length of 30 cm, how much work is required to stretch it from 20 cm to 32 cm?
(Multiple Choice)
4.8/5  (36)
(36)
Sketch the region bounded by the graphs of the given equations and find the area of their region. , ,
(Multiple Choice)
4.8/5  (37)
(37)
Find the number(s) a such that the average value of the function on the interval is equal to 10.
(Multiple Choice)
4.8/5  (42)
(42)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the x-axis. y = cos x + 1, x = 0, y = 0, x =
(Multiple Choice)
4.8/5  (29)
(29)
Find the volume of the solid that is obtained by revolving the region about the line y = . 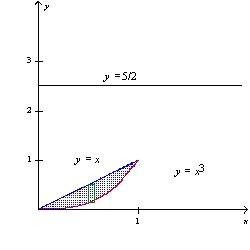
(Multiple Choice)
4.9/5  (38)
(38)
Find the area of the region bounded by the parabola , the tangent line to this parabola at , and the x axis.
(Multiple Choice)
4.7/5  (35)
(35)
Graph the region between the curves and use your calculator to compute the area correct to five decimal places.
(Multiple Choice)
4.9/5  (37)
(37)
Find the volume of the solid obtained by rotating the region bounded by and about the line
(Short Answer)
4.8/5  (34)
(34)
Use the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle.
y = 3 , y = 0, x = 1; the y-axis
(Short Answer)
4.9/5  (31)
(31)
Showing 81 - 95 of 95
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)