Exam 6: Inverse Functions
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
In a certain city the temperature hours after 7 A.M. was modeled by the function Find the average temperature to three decimal places during the period from 7 A.M. to 7 P.M.
(Multiple Choice)
4.7/5  (46)
(46)
Use the method of disks or washers, or the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle.
y = 2 , y = 4x - 2, y = 8; the y-axis
(Short Answer)
4.8/5  (33)
(33)
Find the number b such that the line divides the region bounded by the curves and into two regions with equal area.
(Multiple Choice)
4.8/5  (30)
(30)
The linear density of a m long rod is where x is measured in meters from one end of the rod. Find the average density of the rod.
(Multiple Choice)
4.8/5  (41)
(41)
Sketch a plane region, and indicate the axis about which it is revolved so that the resulting solid of revolution has the volume given by the integral.
(Short Answer)
5.0/5  (39)
(39)
Find the number(s) a such that the average value of the function on the interval is equal to 4 .
(Short Answer)
4.7/5  (32)
(32)
Use the method of cylindrical shells to find the volume of solid obtained by rotating the region bounded by the given curves about the x-axis.
(Multiple Choice)
4.9/5  (36)
(36)
A force of 30 N is required to maintain a spring stretched from its natural length of 12 cm to a length of 15 cm. How much work is done in stretching the spring from 11 cm to 24 cm?
(Multiple Choice)
4.9/5  (26)
(26)
Use cylindrical shells to find the volume of the solid. A sphere of radius .
(Multiple Choice)
5.0/5  (44)
(44)
Find the volume of the solid that is obtained by revolving the region about the x-axis. 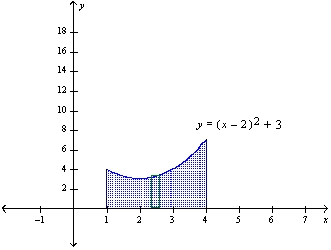
(Multiple Choice)
4.8/5  (39)
(39)
The base of a solid is a circular disk with radius 3 . Find the volume of the solid if parallel cross-sections perpendicular to the base are isosceles right triangles with hypotenuse lying along the base.
(Short Answer)
4.8/5  (37)
(37)
Use the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle. y = , y = -x + 4; the y-axis
(Multiple Choice)
4.8/5  (40)
(40)
The velocity v of blood that flows in a blood vessel with radius and length l at a distance from the central axis is where P is the pressure difference between the ends of the vessel and q is the viscosity of the blood. Find the average velocity (with respect to r) over the interval
(Short Answer)
4.9/5  (42)
(42)
Find the average value of the function on the given interval.
(Multiple Choice)
4.7/5  (35)
(35)
Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line.
(Short Answer)
4.8/5  (32)
(32)
Sketch a graph to estimate the x-coordinates of the points of intersection of the given curves. Then use this information to estimate the volume of the solid obtained by rotating about the y axis the region enclosed by these curves. Rounded to the nearest hundredth.
(Multiple Choice)
4.9/5  (35)
(35)
Use a graphing utility to (a) plot the graphs of the given functions and (b) find the approximate x-coordinates of the points of intersection of the graphs. Then find an approximation of the volume of the solid obtained by revolving the region bounded by the graphs of the functions about the x-axis. Round answers to two decimal places.
y = , y = 3 -
(Short Answer)
4.8/5  (37)
(37)
An aquarium 6 m long, 1 m wide, and 1 m deep is full of water. Find the work needed to pump half of the water out of the aquarium. (Use the facts that the density of water is )
(Multiple Choice)
4.8/5  (36)
(36)
Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line.
(Multiple Choice)
4.8/5  (34)
(34)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated line. y = 4 - , y = 0; the line y = 5
(Multiple Choice)
4.8/5  (32)
(32)
Showing 41 - 60 of 95
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)