Exam 10: Introduction to Differential Equations
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
The differential equation 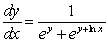 can be solved by which of the following?
can be solved by which of the following?
(Multiple Choice)
4.9/5  (32)
(32)
A deer population for a certain area is initially 350. After 2 years, the population increases to 650. Assuming logistic growth with a carrying capacity of 1200, how long after reaching 650 will it take the population to reach 1000?
(Short Answer)
4.8/5  (36)
(36)
A rat population for a certain field is initially 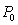 . After 3 years, the population increases to 450. After another 2 years, the population increases to 650. Assuming logistic growth with a carrying capacity of 900, what is
. After 3 years, the population increases to 450. After another 2 years, the population increases to 650. Assuming logistic growth with a carrying capacity of 900, what is 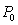 ?
?
(Essay)
4.9/5  (34)
(34)
Use Euler's method with step size 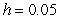 to approximate
to approximate 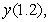 where
where 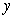 is the solution to the initial value problem
is the solution to the initial value problem 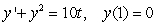 .
.
(Essay)
4.7/5  (36)
(36)
Let 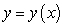 be an increasing function passing through
be an increasing function passing through 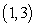 such that the length of the tangent line between the tangency point
such that the length of the tangent line between the tangency point 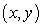 and the y-axis is
and the y-axis is 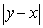 .
. 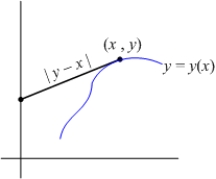 A) Find an initial value problem satisfied by
A) Find an initial value problem satisfied by 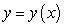 .
B) Use Euler's method with
.
B) Use Euler's method with 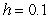 to approximate
to approximate 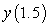 .
.
(Essay)
4.8/5  (37)
(37)
Consider the initial value problem 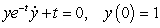 .
A) Use Euler's method with
.
A) Use Euler's method with 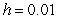 to approximate
to approximate 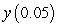 . Give your answer to six decimal places.
B) Solve the initial value problem and find
. Give your answer to six decimal places.
B) Solve the initial value problem and find 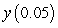 to six decimal places.
C) Compute the error in approximating
to six decimal places.
C) Compute the error in approximating 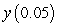 .
.
(Essay)
4.7/5  (37)
(37)
Solve the following differential equations.
A) 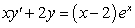 B)
B) 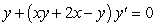 (Hint: rewrite for
(Hint: rewrite for 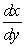 .)
.)
(Essay)
5.0/5  (38)
(38)
A deer population for a certain area is initially 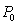 . After 6 years, the population increases to 250. After another 4 years, the population increases to 300. Assuming logistic growth with a carrying capacity of 400, what is
. After 6 years, the population increases to 250. After another 4 years, the population increases to 300. Assuming logistic growth with a carrying capacity of 400, what is 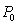 ?
?
(Essay)
4.8/5  (47)
(47)
The differential equation 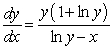 can be solved by which of the following?
can be solved by which of the following?
(Multiple Choice)
4.7/5  (26)
(26)
Solve the differential equations using separation of variables.
A) 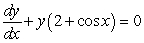 B)
B) 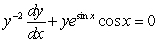
(Essay)
4.9/5  (35)
(35)
Twenty-five rabbits were brought to a zoo 15 years ago.
At present there are 35 rabbits in the zoo. The zoo can support a maximum of 180 rabbits.
Assuming a logistic growth model, when will the rabbit population reach 50, 100, and 180 rabbits?
(Essay)
4.8/5  (40)
(40)
Deer in a certain region, are born at a rate that is proportional to their current population. With the absence of outside factors, the population will double in 3 years' time.
Each year 5 deer join the population, 10 are caught by hunters, and 4 die of natural causes.
If initially there are 50 deer, will the population survive? If not, when will it die out?
(Short Answer)
4.7/5  (30)
(30)
A water tank is obtained by rotating the graph of 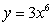 for
for 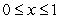 about the y-axis (assume length is measured in meters).
The tank is filled with water and water drains through a circular hole of radius
1 cm at the bottom of the tank.
How long does it take for the tank to empty?
about the y-axis (assume length is measured in meters).
The tank is filled with water and water drains through a circular hole of radius
1 cm at the bottom of the tank.
How long does it take for the tank to empty? 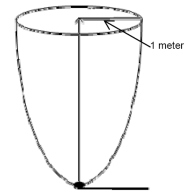
(Short Answer)
4.9/5  (29)
(29)
The differential equation 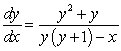 can be solved by which of the following?
can be solved by which of the following?
(Multiple Choice)
4.7/5  (32)
(32)
Showing 21 - 40 of 73
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)