Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 10: Introduction to Differential Equations

arrow
Exam 1: Precalculus Review74 Questionsadd course
Exam 2: Limits97 Questionsadd course
Exam 3: Differentiation81 Questionsadd course
Exam 4: Applications of the Derivative77 Questionsadd course
Exam 5: The Integral82 Questionsadd course
Exam 6: Applications of the Integral80 Questionsadd course
Exam 7: Exponential Functions106 Questionsadd course
Exam 8: Techniques of Integration101 Questionsadd course
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questionsadd course
Exam 10: Introduction to Differential Equations73 Questionsadd course
Exam 11: Infinite Series95 Questionsadd course
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questionsadd course
Exam 13: Vector Geometry96 Questionsadd course
Exam 14: Calculus of Vector-Valued Functions99 Questionsadd course
Exam 15: Differentiation in Several Variables95 Questionsadd course
Exam 16: Multiple Integration98 Questionsadd course
Exam 17: Line and Surface Integrals92 Questionsadd course
Exam 18: Fundamental Theorems of Vector Analysis91 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

Which of the following graphs depicts possible solutions of a logistic equation?

(Multiple Choice)
4.8/5
(40)
Question 41

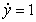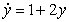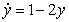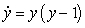Match the differential equation with its slope field. A) Match the differential equation with its slope field. A) B) C) D) E) i) ii) iii) iv) v) B) Match the differential equation with its slope field. A) B) C) D) E) i) ii) iii) iv) v) C) Match the differential equation with its slope field. A) B) C) D) E) i) ii) iii) iv) v) D) Match the differential equation with its slope field. A) B) C) D) E) i) ii) iii) iv) v) E) Match the differential equation with its slope field. A) B) C) D) E) i) ii) iii) iv) v) i) Match the differential equation with its slope field. A) B) C) D) E) i) ii) iii) iv) v) ii) Match the differential equation with its slope field. A) B) C) D) E) i) ii) iii) iv) v) iii) Match the differential equation with its slope field. A) B) C) D) E) i) ii) iii) iv) v) iv) Match the differential equation with its slope field. A) B) C) D) E) i) ii) iii) iv) v) v) Match the differential equation with its slope field. A) B) C) D) E) i) ii) iii) iv) v)

(Short Answer)
4.8/5
(28)
Question 42

Solve the initial value problem. Solve the initial value problem.

(Essay)
4.8/5
(40)
Question 43

An object of constant mass is projected away from the earth with initial velocity An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. (Hint: find such that .) in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. 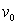(Hint: find such that .) above the earth's surface, the velocity of the object satisfies the differential equation An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. 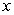(Hint: find such that .) , where An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. (Hint: find such that .) is the radius of the earth. 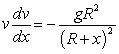An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. 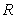(Hint: find such that .) A) Solve for the velocity An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. 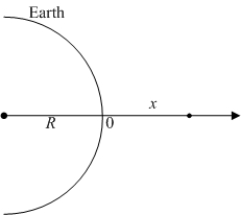(Hint: find such that .) as a function of An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. (Hint: find such that .) . 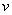B) What is the maximum altitude An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. 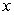(Hint: find such that .) of the object if its initial velocity is An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. (Hint: find such that .) ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. 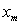(Hint: find An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. (Hint: find such that .) such that An object of constant mass is projected away from the earth with initial velocity in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude above the earth's surface, the velocity of the object satisfies the differential equation , where is the radius of the earth. A) Solve for the velocity as a function of . B) What is the maximum altitude of the object if its initial velocity is ? 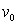C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth. (Hint: find 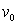such that .) .)

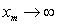(Essay)
4.8/5
(34)
Question 44

Solve the linear equations. A) Solve the linear equations. A) B) (Hint: rewrite for .) B) Solve the linear equations. A) B) (Hint: rewrite for .) (Hint: rewrite for Solve the linear equations. A) B) (Hint: rewrite for .) .)

(Essay)
4.7/5
(37)
Question 45

A 1200-gallon tank initially contains 500 gallons of water with 4 lbs of salt dissolved in it. Water with a salt concentration of 2 lbs/gal enters the tank at a rate of 10 gal/h, while the solution leaves the tank at a rate of 6 gal/h. Find the amount of salt in the tank when it overflows.

(Short Answer)
4.9/5
(34)
Question 46

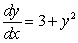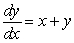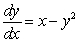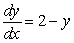Match the direction fields with their differential equations A) Match the direction fields with their differential equations A) B) C) D) i) ii) iii) iv) B) Match the direction fields with their differential equations A) B) C) D) i) ii) iii) iv) C) Match the direction fields with their differential equations A) B) C) D) i) ii) iii) iv) D) Match the direction fields with their differential equations A) B) C) D) i) ii) iii) iv) i) Match the direction fields with their differential equations A) B) C) D) i) ii) iii) iv) ii) Match the direction fields with their differential equations A) B) C) D) i) ii) iii) iv) iii) Match the direction fields with their differential equations A) B) C) D) i) ii) iii) iv) iv) Match the direction fields with their differential equations A) B) C) D) i) ii) iii) iv)

(Short Answer)
4.8/5
(38)
Question 47

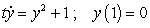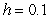Consider the initial value problem. Consider the initial value problem. . A) Use Euler's method with to approximate . Give your answer to six decimal places. A) and B) Use Euler's method with to approximate . Give your answer to six decimal places. B). C) Solve the initial value problem and estimate the error in parts . A) Use Euler's method with Consider the initial value problem. . A) Use Euler's method with to approximate . Give your answer to six decimal places. A) and B) Use Euler's method with to approximate . Give your answer to six decimal places. B). 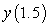C) Solve the initial value problem and estimate the error in parts to approximate Consider the initial value problem. . A) Use Euler's method with to approximate . Give your answer to six decimal places. A) and B) Use Euler's method with to approximate . Give your answer to six decimal places. B). C) Solve the initial value problem and estimate the error in parts . Give your answer to six decimal places. A) and B) Use Euler's method with Consider the initial value problem. . A) Use Euler's method with to approximate . Give your answer to six decimal places. A) and B) Use Euler's method with to approximate . Give your answer to six decimal places. B). C) Solve the initial value problem and estimate the error in parts to approximate Consider the initial value problem. . A) Use Euler's method with to approximate . Give your answer to six decimal places. A) and B) Use Euler's method with 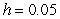to approximate 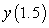. Give your answer to six decimal places. B). C) Solve the initial value problem and estimate the error in parts . Give your answer to six decimal places. B). C) Solve the initial value problem and estimate the error in parts

(Essay)
4.9/5
(38)
Question 48

Bees in a certain region are born at a rate that is proportional to their current population. Without any outside factors the population doubles in 3 weeks' time. It was observed that each day 12 bees joined the population, 10 were caught by men, and 5 died of natural causes. Determine whether the population will survive if initially it counted 100 bees. If not, when will it die out?

(Short Answer)
4.8/5
(29)
Question 49

Solve the differential equation. Solve the differential equation.

(Essay)
4.8/5
(37)
Question 50

Solve the following equations. A) Solve the following equations. A) B) B) Solve the following equations. A) B)

(Essay)
4.8/5
(36)
Question 51

Twenty panda bears were brought to a national park 20 years ago. At present, there are 42 bears in the park. The park can support a maximum of 200 bears. Assuming a logistic growth model, when will the bear population reach 80, 150, and 200 bears?

(Essay)
5.0/5
(34)
Question 52

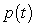Let Let be the population of a certain animal species that satisfies the logistic equation . A) Find the equilibrium solutions and classify them. B) What is the long-term behavior of the population? C) Find the value of at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B. 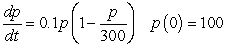be the population of a certain animal species that satisfies the logistic equation Let be the population of a certain animal species that satisfies the logistic equation . A) Find the equilibrium solutions and classify them. B) What is the long-term behavior of the population? C) Find the value of at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B. . A) Find the equilibrium solutions and classify them. B) What is the long-term behavior of the population? C) Find the value of Let be the population of a certain animal species that satisfies the logistic equation . A) Find the equilibrium solutions and classify them. B) What is the long-term behavior of the population? C) Find the value of 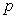at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B. at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B.

(Essay)
4.9/5
(40)
Question 53

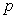Let Let be a population of insects that is modeled by the logistic equation: A) Determine the equilibrium solutions and their stabilities. B) What is the long term behavior of the population? C) Find the value of at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B. 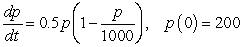be a population of insects that is modeled by the logistic equation: Let be a population of insects that is modeled by the logistic equation: A) Determine the equilibrium solutions and their stabilities. B) What is the long term behavior of the population? C) Find the value of at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B. A) Determine the equilibrium solutions and their stabilities. B) What is the long term behavior of the population? C) Find the value of Let be a population of insects that is modeled by the logistic equation: A) Determine the equilibrium solutions and their stabilities. B) What is the long term behavior of the population? C) Find the value of 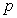at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B. at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B.

(Essay)
4.8/5
(29)
Question 54

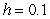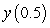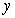Use Euler's method with Use Euler's method with to approximate , where is the solution of the initial value problem . Give your answer to five decimal places. to approximate Use Euler's method with to approximate , where is the solution of the initial value problem . Give your answer to five decimal places. , where Use Euler's method with to approximate , where is the solution of the initial value problem . Give your answer to five decimal places. 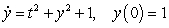is the solution of the initial value problem Use Euler's method with to approximate , where is the solution of the initial value problem . Give your answer to five decimal places. . Give your answer to five decimal places.

(Essay)
4.9/5
(38)
Question 55

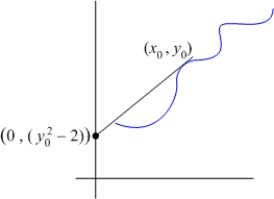
Find all the curves Find all the curves such that the tangent line at any point on the curve has a y-intercept equal to . such that the tangent line at any point Find all the curves such that the tangent line at any point on the curve has a y-intercept equal to . on the curve has a y-intercept equal to Find all the curves such that the tangent line at any point on the curve has a y-intercept equal to . . Find all the curves 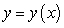such that the tangent line at any point 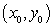on the curve has a y-intercept equal to .

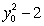(Essay)
4.8/5
(33)
Question 56

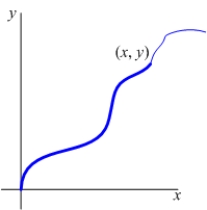
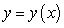The graph of an increasing function The graph of an increasing function passes through the origin, and the arc length between the points and on the graph is . A) Write an initial value problem satisfied by . B) Use Euler's method with to estimate . passes through the origin, and the arc length between the points The graph of an increasing function passes through the origin, and the arc length between the points and on the graph is . A) Write an initial value problem satisfied by . B) Use Euler's method with to estimate . 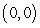and The graph of an increasing function passes through the origin, and the arc length between the points and on the graph is . A) Write an initial value problem satisfied by . B) Use Euler's method with to estimate . 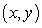on the graph is The graph of an increasing function passes through the origin, and the arc length between the points and on the graph is . A) Write an initial value problem satisfied by . B) Use Euler's method with to estimate . . 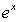A) Write an initial value problem satisfied by The graph of an increasing function passes through the origin, and the arc length between the points and on the graph is . A) Write an initial value problem satisfied by . B) Use Euler's method with to estimate . . 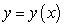B) Use Euler's method with The graph of an increasing function passes through the origin, and the arc length between the points and on the graph is . A) Write an initial value problem satisfied by . B) Use Euler's method with to estimate . to estimate The graph of an increasing function passes through the origin, and the arc length between the points and on the graph is . A) Write an initial value problem satisfied by . B) Use Euler's method with to estimate . . The graph of an increasing function passes through the origin, and the arc length between the points and on the graph is . A) Write an initial value problem satisfied by . B) Use Euler's method with 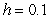to estimate .

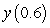(Essay)
4.8/5
(28)
Question 57

The curves orthogonal to the solutions of The curves orthogonal to the solutions of are: are:

(Multiple Choice)
4.8/5
(35)
Question 58

The differential equation The differential equation is: is:

(Multiple Choice)
4.8/5
(35)
Question 59

Solve the differential equation. Solve the differential equation.

(Essay)
4.8/5
(28)
Question 60
Showing 41 - 60 of 73
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)