Exam 10: Introduction to Differential Equations
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Consider the initial value problem 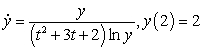 A) Use Euler's method with
A) Use Euler's method with 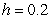 to approximate
to approximate 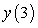 . Give your answer to five decimal places.
B) Solve the initial value problem and compute
. Give your answer to five decimal places.
B) Solve the initial value problem and compute 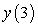 to five decimal places.
C) Compute the error in the approximation of
to five decimal places.
C) Compute the error in the approximation of 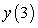 .
.
(Essay)
5.0/5  (27)
(27)
A rat population in a certain field is initially 200. After 4 years, the population increases to 350. Assuming logistic growth with a carrying capacity of 550, what is the rat population 3 years after the population reached 350?
(Short Answer)
4.8/5  (34)
(34)
A certain chemical dissolves in water at a rate proportional to the product of the amount of chemical that had not yet been dissolved and the difference between its concentration in a saturated solution and its current concentration.
It is known that 100 g of the chemical are dissolved in 200 g of saturated solution. If 60 g of the chemical are added to 200 g of water, 20 g are dissolved in 2 h.
How many grams of the chemical are dissolved in 4 h?
(Short Answer)
4.7/5  (27)
(27)
Use the following steps.
A) Write an equation for the areas using integrals.
B) Differentiate the equation in A and solve the resulting linear equation.
Ans:
A) 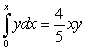 B)
B) 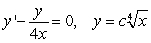 -A pool contains 12 million gal of fresh water. Contaminated water flows into the pool at a rate of 4 million gal/year as the mixture in the pool flows out at the same rate.
The concentration
-A pool contains 12 million gal of fresh water. Contaminated water flows into the pool at a rate of 4 million gal/year as the mixture in the pool flows out at the same rate.
The concentration 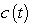 of the chemical in the incoming contaminated water is
of the chemical in the incoming contaminated water is 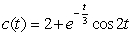 g/gal, where t is in years.
Find the amount
g/gal, where t is in years.
Find the amount  of the chemical in the pool at time
of the chemical in the pool at time  .
.
(Essay)
4.7/5  (31)
(31)
Solving the differential equation 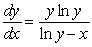 , we obtain the solution:
, we obtain the solution:
(Multiple Choice)
4.7/5  (32)
(32)
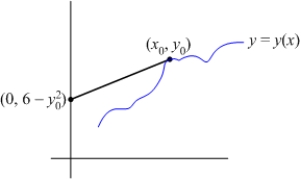
Find all curves 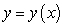 such that the tangent line at any point
such that the tangent line at any point 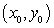 on the curve has a y-intercept that is equal to
on the curve has a y-intercept that is equal to 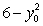 .
. 
(Essay)
5.0/5  (40)
(40)
The horizontal cross sections at height 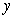 of a tank are discs of radius
of a tank are discs of radius 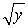 . The height of the tank is 10 m.
The tank is filled with water, and the water drains through a square hole with a side of 10 cm at the bottom of the tank.
How long does it take for the tank to empty?
. The height of the tank is 10 m.
The tank is filled with water, and the water drains through a square hole with a side of 10 cm at the bottom of the tank.
How long does it take for the tank to empty? 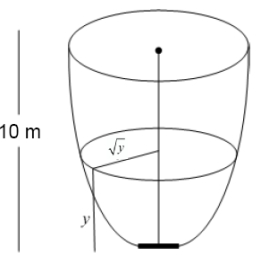
(Short Answer)
5.0/5  (32)
(32)
A deer population for a certain area is initially 500. After 3 years, the population increases to 600. Assuming logistic growth with a carrying capacity of 850, what is the deer population 2 years after the population reached 600?
(Short Answer)
4.8/5  (32)
(32)
Match the differential equation with its slope field.
A) 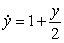 B)
B) 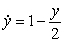 C)
C) 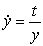 i)
i)  ii)
ii)  iii)
iii) 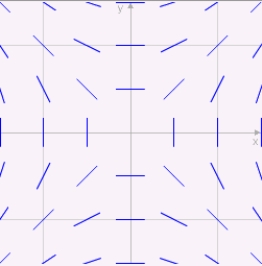
(Short Answer)
4.8/5  (36)
(36)
Consider the logistic equation 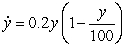 . The solution with the following initial condition is decreasing to minus infinity at a finite value of
. The solution with the following initial condition is decreasing to minus infinity at a finite value of 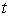 :
:
(Multiple Choice)
4.8/5  (41)
(41)
Match the differential equation with its slope field
(A) 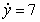 (B)
(B) 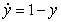 (C)
(C) 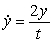 i)
i)  ii)
ii) 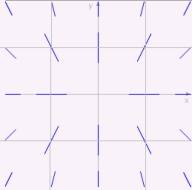 iii)
iii) 
(Short Answer)
4.8/5  (35)
(35)
Showing 61 - 73 of 73
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)