Exam 9: Further Applications of the Integral and Taylor Polynomials
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
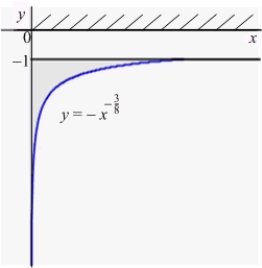
An infinite plate shown in the figure below, bounded by the graphs of 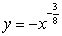 and
and 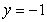 and the y-axis, is submerged vertically in water, with its top
and the y-axis, is submerged vertically in water, with its top 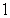 ft below the water surface.
Calculate the fluid force on a side of the plate. (The density of water is
ft below the water surface.
Calculate the fluid force on a side of the plate. (The density of water is 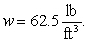 )
) 
(Essay)
4.9/5  (33)
(33)
A plate bounded by the functions 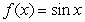 and
and 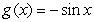 on the interval
on the interval 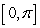 is submerged vertically so that the top of the plate is under 1 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 1 m of water. What is the fluid force on the side of the plate?
(Short Answer)
4.7/5  (34)
(34)
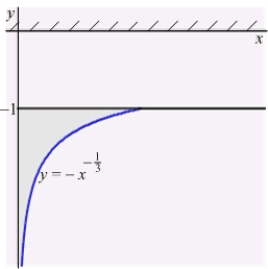
An infinite plate shown in the figure below, bounded by the graphs of 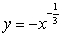 and
and 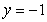 and the y-axis, is submerged vertically in water, with its top
and the y-axis, is submerged vertically in water, with its top 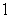 ft below the water surface.
Calculate the fluid force on a side of the plate. (The density of water is
ft below the water surface.
Calculate the fluid force on a side of the plate. (The density of water is 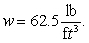 )
) 
(Essay)
4.9/5  (45)
(45)
Let 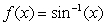 .
A) Write the Maclaurin polynomial
.
A) Write the Maclaurin polynomial 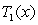 for
for 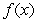 .
B) Use Taylor's Theorem for
.
B) Use Taylor's Theorem for 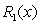 to write an integration formula.
to write an integration formula.
(Essay)
4.8/5  (35)
(35)
Find 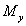 for the lamina of uniform density
for the lamina of uniform density 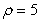 occupying the region under
occupying the region under 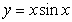 from
from 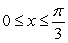 .
.
(Essay)
5.0/5  (28)
(28)
Let 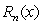 denote the
denote the 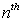 remainder
remainder 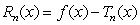 , where
, where 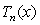 is the
is the 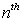 Maclaurin polynomial for
Maclaurin polynomial for 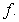 If
If 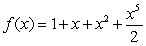 , find
, find 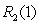 .
.
(Essay)
4.8/5  (40)
(40)
Compute 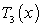 for
for 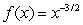 centered at
centered at 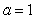 . Use the error bound to find the maximum possible size of error of
. Use the error bound to find the maximum possible size of error of 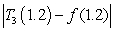 .
.
(Essay)
4.8/5  (36)
(36)
Find the centroid of the portion of the unit circle lying within the first three quadrants.
(Essay)
4.8/5  (44)
(44)
Compute the surface area of revolution of 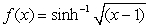 about the x-axis over the interval
about the x-axis over the interval 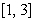 .
.
(Short Answer)
4.7/5  (34)
(34)
Showing 21 - 40 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)