Exam 9: Further Applications of the Integral and Taylor Polynomials
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Find the surface area of the ellipsoid obtained by rotating the ellipse 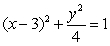 about the x-axis.
about the x-axis.
(Short Answer)
4.8/5  (30)
(30)
Approximate the arc length of the curve 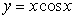 over the interval
over the interval 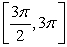 using the Trapezoidal Rule
using the Trapezoidal Rule 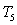 .
.
(Short Answer)
4.9/5  (27)
(27)
The plate shown in the figure, enclosed by the curves 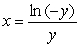 ,
, 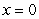 , and
, and 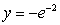 , is submerged vertically in a fluid with density
, is submerged vertically in a fluid with density 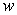 so that its top is at a depth of
so that its top is at a depth of 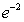 . Find the fluid pressure on a side of the plate if
. Find the fluid pressure on a side of the plate if 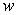 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 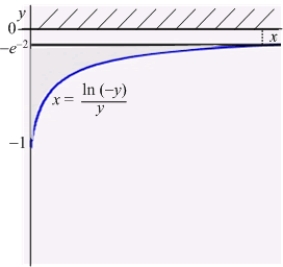
(Essay)
4.9/5  (38)
(38)
Let 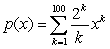 .
What is the coefficient of
.
What is the coefficient of 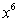 in the sixth Maclaurin polynomial for
in the sixth Maclaurin polynomial for 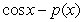 ?
?
(Essay)
4.8/5  (40)
(40)
Five particles of equal mass are located at 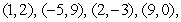 and
and 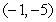 . Find the center of mass of the system.
. Find the center of mass of the system.
(Essay)
4.8/5  (37)
(37)
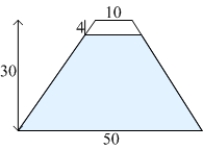
The face of a dam is an isosceles trapezoid of height 30 ft and bases 10 ft and 50 ft. The dam is oriented vertically with the larger base at the bottom. Find the force on the dam if the water level is 4 ft below the top of the dam. (The density of the water is 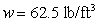 .)
.) 
(Essay)
4.8/5  (42)
(42)
Let 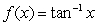 .
A) Write the Maclaurin polynomial
.
A) Write the Maclaurin polynomial 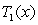 for
for 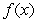 .
B) Use Taylor's Theorem for
.
B) Use Taylor's Theorem for 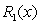 to write an integration formula for
to write an integration formula for 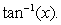
(Essay)
4.9/5  (41)
(41)
Use implicit differentiation to compute the surface area of revolution about the x-axis of the part of the astroid 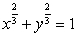 in the first quadrant.
in the first quadrant. 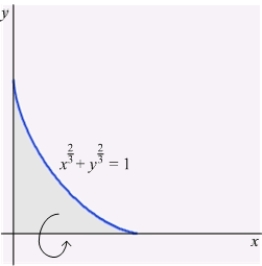
(Essay)
4.9/5  (45)
(45)
Compute the surface area of revolution of 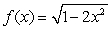 about the x-axis over the interval
about the x-axis over the interval 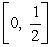 .
.
(Short Answer)
4.7/5  (42)
(42)
Use additivity of moments to find the center of mass of the region consisting of a semicircle on top of an isosceles trapezoid of height 1 and bases 2 and 4, as shown below. 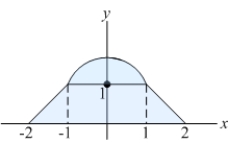
(Essay)
4.8/5  (36)
(36)
A thin plate shown in the following figure is bounded by the graphs of 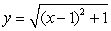 and
and 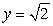 . The plate is submerged in a fluid with density
. The plate is submerged in a fluid with density  so that its top is level with the surface of the fluid.
Calculate the fluid pressure on a side of the plate if
so that its top is level with the surface of the fluid.
Calculate the fluid pressure on a side of the plate if  is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 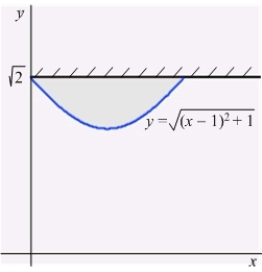
(Essay)
4.8/5  (36)
(36)
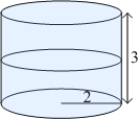
A water tank is a cylinder 4 ft in diameter, standing on its base. If water fills the tank to a depth of 3 ft, what is the magnitude of the force exerted on the side of the tank? (The density of the water is 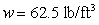 .)
.) 
(Essay)
4.9/5  (41)
(41)
In the following figure, the centroid of the region enclosed by the graphs of 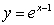 ,
, 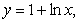 and
and 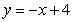 lies on:
lies on: 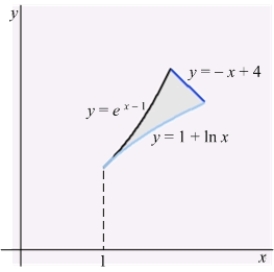
(Multiple Choice)
4.9/5  (42)
(42)
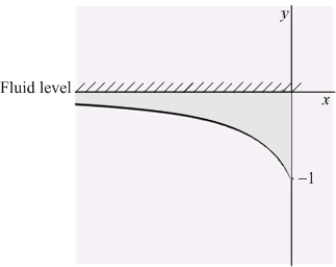
An infinite plate shown in the figure below, bounded by the graphs of 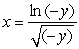 and
and 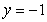 and the two axes, is submerged vertically in a fluid with density
and the two axes, is submerged vertically in a fluid with density 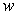 in kilograms per cubic meter; its top is level with the fluid surface.
Calculate the fluid force on a side of the plate and write the answer in terms of
in kilograms per cubic meter; its top is level with the fluid surface.
Calculate the fluid force on a side of the plate and write the answer in terms of 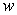 and
and 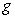 .
. 
(Essay)
4.9/5  (40)
(40)
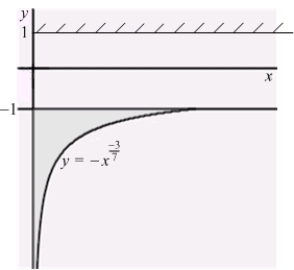
An infinite plate shown in the figure below, bounded by the graphs of 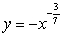 ,
, 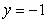 , and the y-axis, is submerged vertically in water, with its top
, and the y-axis, is submerged vertically in water, with its top 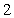 ft below the water surface. Calculate the fluid force on a side of the plate.
(The density of water is
ft below the water surface. Calculate the fluid force on a side of the plate.
(The density of water is 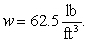 )
) 
(Short Answer)
4.7/5  (36)
(36)
Showing 41 - 60 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)