Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 4: Applications of the Derivative

arrow
Exam 1: Precalculus Review74 Questionsadd course
Exam 2: Limits97 Questionsadd course
Exam 3: Differentiation81 Questionsadd course
Exam 4: Applications of the Derivative77 Questionsadd course
Exam 5: The Integral82 Questionsadd course
Exam 6: Applications of the Integral80 Questionsadd course
Exam 7: Exponential Functions106 Questionsadd course
Exam 8: Techniques of Integration101 Questionsadd course
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questionsadd course
Exam 10: Introduction to Differential Equations73 Questionsadd course
Exam 11: Infinite Series95 Questionsadd course
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questionsadd course
Exam 13: Vector Geometry96 Questionsadd course
Exam 14: Calculus of Vector-Valued Functions99 Questionsadd course
Exam 15: Differentiation in Several Variables95 Questionsadd course
Exam 16: Multiple Integration98 Questionsadd course
Exam 17: Line and Surface Integrals92 Questionsadd course
Exam 18: Fundamental Theorems of Vector Analysis91 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

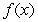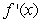What can you conclude about the graph of What can you conclude about the graph of from the following table? -1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on from the following table? -1 -6 What can you conclude about the graph of from the following table? 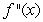-1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on + 0 - - - What can you conclude about the graph of from the following table? 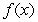-1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on + 0 - 0 - A) What can you conclude about the graph of from the following table? 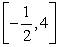-1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on is concave down on What can you conclude about the graph of from the following table? 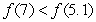-1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on and What can you conclude about the graph of from the following table? 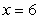-1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on B) What can you conclude about the graph of from the following table? 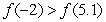-1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on is an inflection point and What can you conclude about the graph of from the following table? 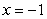-1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on C) What can you conclude about the graph of from the following table? 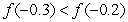-1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on is an inflection point and What can you conclude about the graph of from the following table? 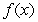-1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on D) What can you conclude about the graph of from the following table? 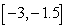-1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on is concave up on What can you conclude about the graph of from the following table? -1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on and What can you conclude about the graph of from the following table? -1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and is increasing on is increasing on What can you conclude about the graph of from the following table? -1 -6 + 0 - - - + 0 - 0 - A) is concave down on and B) is an inflection point and C) is an inflection point and D) is concave up on and 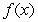is increasing on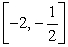

(Short Answer)
4.8/5
(33)
Question 61

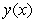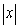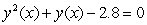Suppose that a function Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in to 4 decimal digits using linearization for . satisfies the following equation for small values of Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in to 4 decimal digits using linearization for . 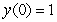: Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in to 4 decimal digits using linearization for . . 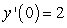Also, Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in to 4 decimal digits using linearization for . 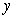and Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in to 4 decimal digits using linearization for . . 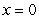A) Find the linearization of Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in to 4 decimal digits using linearization for . 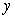at Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in to 4 decimal digits using linearization for . . 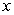B) Replace Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in to 4 decimal digits using linearization for . by its linearization and find a quadratic equation for Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in to 4 decimal digits using linearization for . . C) Estimate the roots of the quadratic equation in Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in to 4 decimal digits using linearization for . to 4 decimal digits using linearization for Suppose that a function satisfies the following equation for small values of : . Also, and . A) Find the linearization of at . B) Replace by its linearization and find a quadratic equation for . C) Estimate the roots of the quadratic equation in 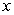to 4 decimal digits using linearization for . .

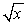(Essay)
4.7/5
(41)
Question 62

The radius The radius of a sphere is measured at 4 m. Use linear approximation to estimate the maximum error in the surface area of the sphere if is accurate to within m. of a sphere is measured at 4 m. Use linear approximation to estimate the maximum error in the surface area of the sphere if The radius of a sphere is measured at 4 m. Use linear approximation to estimate the maximum error in the surface area of the sphere if is accurate to within m. is accurate to within The radius 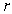of a sphere is measured at 4 m. Use linear approximation to estimate the maximum error in the surface area of the sphere if 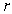is accurate to within 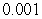m. m.

(Essay)
4.7/5
(47)
Question 63

Sketch the graph of the function. Indicate the asymptotes, local extrema, and points of inflection. Sketch the graph of the function. Indicate the asymptotes, local extrema, and points of inflection.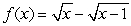

(Essay)
4.9/5
(41)
Question 64

Apply Newton's Method to Apply Newton's Method to with an initial guess of to calculate , , and . with an initial guess of Apply Newton's Method to with an initial guess of to calculate , , and . to calculate Apply Newton's Method to with an initial guess of to calculate , , and . , Apply Newton's Method to 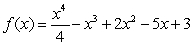with an initial guess of 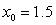to calculate 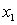, , 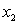and . , and Apply Newton's Method to with an initial guess of to calculate , , and . .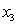

(Essay)
4.9/5
(35)
Question 65

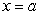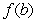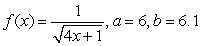Find the linearization of the given function centered at Find the linearization of the given function centered at , and use it to estimate . A) B) , and use it to estimate Find the linearization of the given function centered at , and use it to estimate . A) B) . A) Find the linearization of the given function centered at , and use it to estimate . A) B) B) Find the linearization of the given function centered at , and use it to estimate . A) B)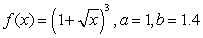

(Essay)
4.8/5
(47)
Question 66

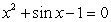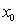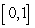Show that the equation Show that the equation has a root in the interval and use Newton's Method to approximate it to four decimal places. has a root Show that the equation has a root in the interval and use Newton's Method to approximate it to four decimal places. in the interval Show that the equation has a root in the interval and use Newton's Method to approximate it to four decimal places. and use Newton's Method to approximate it to four decimal places.

(Essay)
4.9/5
(31)
Question 67

Use Newton's Method to approximate the only positive root for Use Newton's Method to approximate the only positive root for to within an error of at most to within an error of at most Use Newton's Method to approximate the only positive root for 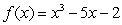to within an error of at most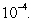

(Short Answer)
4.8/5
(45)
Question 68

Find the intervals on which the function is concave up and concave down and indicate the points of inflection A) Find the intervals on which the function is concave up and concave down and indicate the points of inflection A) 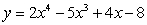B) B) Find the intervals on which the function is concave up and concave down and indicate the points of inflection A) B)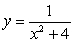

(Essay)
4.8/5
(39)
Question 69

The minimum and maximum of which of the following functions does not occur at a critical point in the open interval:

(Multiple Choice)
4.8/5
(36)
Question 70

Show that the equation Show that the equation has a root in the interval and use Newton's Method to approximate it with an error of at most . has a root in the interval Show that the equation has a root in the interval and use Newton's Method to approximate it with an error of at most . and use Newton's Method to approximate it with an error of at most Show that the equation 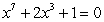has a root in the interval 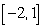and use Newton's Method to approximate it with an error of at most . .

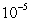(Essay)
4.9/5
(34)
Question 71

Find all the critical points of the function A) Find all the critical points of the function A) B) B) Find all the critical points of the function A) B)

(Essay)
4.8/5
(40)
Question 72

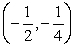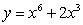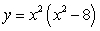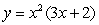Which of the following functions has a local maximum at a point in the interval Which of the following functions has a local maximum at a point in the interval : A) B) C) D) : A) Which of the following functions has a local maximum at a point in the interval : A) B) C) D) B) Which of the following functions has a local maximum at a point in the interval : A) B) C) D) C) Which of the following functions has a local maximum at a point in the interval : A) B) C) D) D) Which of the following functions has a local maximum at a point in the interval : A) B) C) D)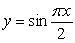

(Essay)
4.8/5
(37)
Question 73

Estimate Estimate using linear approximation. using linear approximation.

(Essay)
4.9/5
(36)
Question 74

Find the intervals on which the function is concave up and concave down and indicate the points of inflection A) Find the intervals on which the function is concave up and concave down and indicate the points of inflection A) 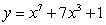B) B) Find the intervals on which the function is concave up and concave down and indicate the points of inflection A) B)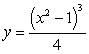

(Essay)
4.7/5
(40)
Question 75

The following is the graph of The following is the graph of Where do the points of inflection of occur, and on which intervals is concave up? Where do the points of inflection of The following is the graph of Where do the points of inflection of occur, and on which intervals is concave up? occur, and on which intervals is The following is the graph of Where do the points of inflection of occur, and on which intervals is concave up? concave up? The following is the graph of 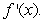Where do the points of inflection of 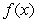occur, and on which intervals is 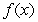concave up?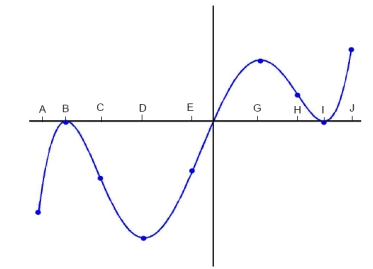

(Essay)
4.7/5
(34)
Question 76

Estimate the roots of the equation Estimate the roots of the equation using the linear approximation for . using the linear approximation for Estimate the roots of the equation 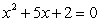using the linear approximation for . .

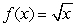(Essay)
4.7/5
(44)
Question 77
Showing 61 - 77 of 77
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)