Exam 13: Inference About Comparing Two Populations, Part 2
Exam 1: What Is Statistics39 Questions
Exam 2: Graphical and Tabular Descriptive Techniques192 Questions
Exam 3: Numerical Descriptive Techniques215 Questions
Exam 4: Data Collection and Sampling82 Questions
Exam 5: Probability200 Questions
Exam 6: Random Variables and Discrete Probability Distributions158 Questions
Exam 7: Continuous Probability Distributions149 Questions
Exam 8: Sampling Distributions127 Questions
Exam 9: Introduction to Estimation85 Questions
Exam 10: Introduction to Hypothesis Testing178 Questions
Exam 11: Inference About a Population75 Questions
Exam 12: Inference About Comparing Two Populations, Part 183 Questions
Exam 13: Inference About Comparing Two Populations, Part 284 Questions
Exam 14: Analysis of Variance125 Questions
Exam 15: Chi-Squared Tests118 Questions
Exam 16: Simple Linear Regression and Correlation231 Questions
Exam 17: Multiple Regression143 Questions
Exam 18: Review of Statistical Inference182 Questions
Select questions type
Antioxidants: A food processor wants to compare two antioxidants for their effects on retarding spoilage. Suppose 16 cuts of fresh meat are treated with antioxidant A and 16 are treated with antioxidant B, and the number of hours until spoilage begins is recorded for each of the 32 cuts of meat. The results are summarized in the table below
 -Develop the 95% confidence interval estimate of the ratio of the two population variances.
-Develop the 95% confidence interval estimate of the ratio of the two population variances.
(Essay)
4.8/5  (37)
(37)
Mass Production Line: A quality control examiner keeps a tally sheet of the number of acceptable and unacceptable products that come off two different production lines. The completed sheet is shown below.
 -What is the p-value of the test? Explain how to use it for testing the hypotheses.
-What is the p-value of the test? Explain how to use it for testing the hypotheses.
(Essay)
4.7/5  (36)
(36)
In constructing a confidence interval estimate for the difference between two population proportions, we pool the population proportions when the populations are normally distributed.
(True/False)
4.9/5  (37)
(37)
A councilwoman regularly polls her constituency to gauge her level of support among voters. This month, 652 out of 1158 voters support her. Five months ago, 412 out of 982 voters supported her. With a 5% significance level, can she infer that support has increased by at least 10 percentage points?
(Essay)
4.9/5  (28)
(28)
Antioxidants: A food processor wants to compare two antioxidants for their effects on retarding spoilage. Suppose 16 cuts of fresh meat are treated with antioxidant A and 16 are treated with antioxidant B, and the number of hours until spoilage begins is recorded for each of the 32 cuts of meat. The results are summarized in the table below
 -Determine the rejection region for testing the equality of the two population variances at = 0.05.
-Determine the rejection region for testing the equality of the two population variances at = 0.05.
(Essay)
4.8/5  (35)
(35)
When comparing two population variances, we use the ratio 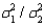 rather than the difference
rather than the difference 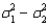 .
.
(True/False)
4.7/5  (32)
(32)
When testing for the difference between two population variances with sample sizes of n1 = 8 and n2 = 10, the degrees of freedom are:
(Multiple Choice)
4.8/5  (36)
(36)
Profit Margin: An investor is considering two types of investment. She is quite satisfied that the expected profit margin on Investment 1 is higher than the expected profit margin on Investment 2. However, she is quite concerned that the risk associated with Investment 1 is higher than that of Investment 2. To help make her decision, she randomly selects seven monthly profit margins on investment 1 and ten monthly profit margins on investment 2. She finds that the sample variances of Investments 1 and 2 are 225 and 118, respectively.
-Estimate with 95% confidence the ratio of the two population variances.
(Essay)
4.8/5  (35)
(35)
The difference in two sample proportions is an unbiased consistent estimator of the difference in their respective population proportions.
(True/False)
4.8/5  (26)
(26)
To estimate the ratio of the population variances you use the ____________________ of the ____________________ variances.
(Short Answer)
4.9/5  (29)
(29)
Senatorial Election: A political poll immediately prior to a senatorial election reveals that 145 out of 250 male voters and 105 out of 200 female voters intend to vote for the Democrat candidate.
-What is the p-value of the test?
(Essay)
4.7/5  (41)
(41)
Speed Limits Violation: Do out-of-state motorists violate the speed limit more frequently than in-state motorists? This vital question was addressed by the highway patrol in a large eastern state. A random sample of the speeds of 2,500 randomly selected cars was categorized according to whether the car was registered in the state or in some other state and whether or not the car was violating the speed limit. The data follow.
 -Do these data provide enough evidence to support the highway patrol's claim at the 5% significance level?
-Do these data provide enough evidence to support the highway patrol's claim at the 5% significance level?
(Essay)
4.8/5  (35)
(35)
The test for the equality of two population variances assumes that each of the two populations is normally distributed.
(True/False)
4.8/5  (31)
(31)
The expected value of the difference between two sample proportions is the ____________________ of/between their corresponding population proportions.
(Short Answer)
4.7/5  (39)
(39)
The difference in two sample proportions is a(n) ____________________ estimator of the difference in their respective population proportions.
(Short Answer)
4.7/5  (36)
(36)
Headache Medicine: A researcher wants to see if/how men and women differ in their reaction to a headache medicine with respect to drowsiness. In testing the hypotheses 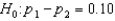 vs.
vs. 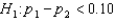 , the following statistics were obtained: n1 = 400, x1 = 208, n2 = 250, and x2 = 115, where x1 and x2 represent the number of patients in the two samples (men vs. women) who reported to have drowsiness as a result of taking headache medicine.
-What conclusion can we draw at the 10% significance level?
, the following statistics were obtained: n1 = 400, x1 = 208, n2 = 250, and x2 = 115, where x1 and x2 represent the number of patients in the two samples (men vs. women) who reported to have drowsiness as a result of taking headache medicine.
-What conclusion can we draw at the 10% significance level?
(Essay)
4.9/5  (47)
(47)
The F-test used for testing the difference in 2 population variances is always a one-tailed test.
(True/False)
4.9/5  (40)
(40)
The expected value of the difference between two sample proportions is the difference between their corresponding population proportions.
(True/False)
4.7/5  (29)
(29)
The test statistic employed to test 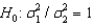 is
is 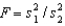 is F-distributed with v1 = n1 - 1 and v2 = n2 - 1 degrees of freedom if the two populations are F-distributed.
is F-distributed with v1 = n1 - 1 and v2 = n2 - 1 degrees of freedom if the two populations are F-distributed.
(True/False)
4.8/5  (34)
(34)
Showing 41 - 60 of 84
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)