Exam 13: Inference About Comparing Two Populations, Part 2
Exam 1: What Is Statistics39 Questions
Exam 2: Graphical and Tabular Descriptive Techniques192 Questions
Exam 3: Numerical Descriptive Techniques215 Questions
Exam 4: Data Collection and Sampling82 Questions
Exam 5: Probability200 Questions
Exam 6: Random Variables and Discrete Probability Distributions158 Questions
Exam 7: Continuous Probability Distributions149 Questions
Exam 8: Sampling Distributions127 Questions
Exam 9: Introduction to Estimation85 Questions
Exam 10: Introduction to Hypothesis Testing178 Questions
Exam 11: Inference About a Population75 Questions
Exam 12: Inference About Comparing Two Populations, Part 183 Questions
Exam 13: Inference About Comparing Two Populations, Part 284 Questions
Exam 14: Analysis of Variance125 Questions
Exam 15: Chi-Squared Tests118 Questions
Exam 16: Simple Linear Regression and Correlation231 Questions
Exam 17: Multiple Regression143 Questions
Exam 18: Review of Statistical Inference182 Questions
Select questions type
Headache Medicine: A researcher wants to see if/how men and women differ in their reaction to a headache medicine with respect to drowsiness. In testing the hypotheses 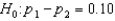 vs.
vs. 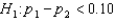 , the following statistics were obtained: n1 = 400, x1 = 208, n2 = 250, and x2 = 115, where x1 and x2 represent the number of patients in the two samples (men vs. women) who reported to have drowsiness as a result of taking headache medicine.
-Estimate with 90% confidence the difference between the two population proportions.
, the following statistics were obtained: n1 = 400, x1 = 208, n2 = 250, and x2 = 115, where x1 and x2 represent the number of patients in the two samples (men vs. women) who reported to have drowsiness as a result of taking headache medicine.
-Estimate with 90% confidence the difference between the two population proportions.
(Essay)
4.9/5  (26)
(26)
The variance of the difference in sample proportions equals the difference of their population variances.
(True/False)
4.8/5  (37)
(37)
When the necessary conditions are met, a two-tail test is being conducted at = 0.05 to test 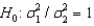 . The two sample variances are
. The two sample variances are 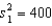 and
and 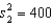 , and the sample sizes are n1 = 25 and n2 = 25. The calculated value of the test statistic will be F = 2.
, and the sample sizes are n1 = 25 and n2 = 25. The calculated value of the test statistic will be F = 2.
(True/False)
5.0/5  (36)
(36)
Showing 81 - 84 of 84
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)