Exam 11: Statistical Inferences Based on Two Samples
Exam 1: An Introduction to Business Statistics and Analytics98 Questions
Exam 2: Descriptive Statistics and Analytics: Tabular and Graphical Methods120 Questions
Exam 3: Descriptive Statistics and Analytics: Numerical Methods145 Questions
Exam 4: Probability and Probability Models150 Questions
Exam 5: Predictive Analytics I: Trees, K-Nearest Neighbors, Naive Bayes,101 Questions
Exam 6: Discrete Random Variables150 Questions
Exam 7: Continuous Random Variables150 Questions
Exam 8: Sampling Distributions111 Questions
Exam 9: Confidence Intervals149 Questions
Exam 10: Hypothesis Testing150 Questions
Exam 11: Statistical Inferences Based on Two Samples140 Questions
Exam 12: Experimental Design and Analysis of Variance132 Questions
Exam 13: Chi-Square Tests120 Questions
Exam 14: Simple Linear Regression Analysis147 Questions
Exam 15: Multiple Regression and Model Building85 Questions
Exam 16: Predictive Analytics Ii: Logistic Regression, Discriminate Analysis,101 Questions
Exam 17: Time Series Forecasting and Index Numbers161 Questions
Exam 18: Nonparametric Methods103 Questions
Exam 19: Decision Theory90 Questions
Select questions type
When we test H0: p1 − p2 ≤ .01, HA: p1 − p2 > .01, at α = .05, where 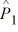 = .08,
= .08, 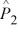 = .035,
n1 = 200, and n2= 400, what is the standard deviation used to calculate the test statistic?
= .035,
n1 = 200, and n2= 400, what is the standard deviation used to calculate the test statistic?
(Short Answer)
4.8/5  (33)
(33)
A fast-food company uses two management-training methods. Method 1 is a traditional method of training, and Method 2 is a new and innovative method. The company has just hired 31 new management trainees. 15 of the trainees are randomly selected and assigned to the first method, and the remaining 16 trainees are assigned to the second training method. After three months of training, the management trainees take a standardized test. The test was designed to evaluate their performance and learning from training. The sample mean score and sample standard deviation of the two methods are given below. The management wants to determine if the company should implement the new training method.
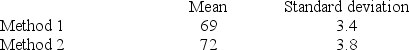 Is there evidence at α = .05 to conclude that the new training method is more effective than the traditional training method?
Is there evidence at α = .05 to conclude that the new training method is more effective than the traditional training method?
(Short Answer)
4.8/5  (35)
(35)
A test of mathematical ability is given to a random sample of 10 eighth-grade students before and after they complete a semester-long basic mathematics course. The mean score before the course was 119.60, and after the course the mean score was 130.80. The standard deviation of the difference is 16.061. What do you conclude at α = .01? Use confidence intervals to draw your conclusion.
(Short Answer)
4.9/5  (39)
(39)
The test of means for two related populations matches the observations (matched pairs) in order to reduce the ________ attributable to the difference between individual observations and other factors.
(Multiple Choice)
4.9/5  (40)
(40)
If we are testing the hypothesis about the mean of a population of paired differences with samples of n1 = 8, n2 = 8, the degrees of freedom for the t statistic is ________.
(Multiple Choice)
4.8/5  (40)
(40)
Find a 95 percent confidence interval for the difference between the proportions of people who prefer cola versus root beer (RB), where  cola = .21,
cola = .21, 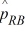 = .12, ncola = 200, and nRB = 150.
= .12, ncola = 200, and nRB = 150.
(Short Answer)
4.9/5  (32)
(32)
The registrar at a state college is interested in determining whether there is a difference of more than one credit hour between male and female students in the average number of credit hours taken during a term. She selected a random sample of 60 male and 60 female students and observed the following sample information.
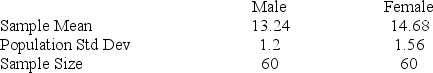 Calculate the test statistic to be used in the analysis. Assume unequal variances.
Calculate the test statistic to be used in the analysis. Assume unequal variances.
(Short Answer)
4.8/5  (38)
(38)
The exact shape of the curve of the F distribution depends on two parameters, df1 and df2.
(True/False)
4.7/5  (32)
(32)
Calculate the pooled variance where sample 1 has data: 16, 14, 19, 18, 19, 20, 15, 18, 17, 18; and sample 2 has data: 13, 19, 14, 17, 21, 14, 15, 10, 13, 15.
(Short Answer)
4.8/5  (42)
(42)
A financial analyst working for a financial consulting company wishes to find evidence that the average price-to-earnings ratio in the consumer industry is higher than the average price-to-earnings ratio in the banking industry. The alternative hypothesis is
(Multiple Choice)
4.9/5  (36)
(36)
Coach Z, the mid-distance running coach for the Olympic team of an eastern European country, claims that his six-month training program significantly reduces the average time to complete a 1500-meter run. Five mid-distance runners were randomly selected. Their times (in minutes) for the 1500-meter run were recorded before and after six months of training under Coach Z. The results are given below.
 At an alpha level of .05, can we conclude that there has been a significant decrease in the meantime?
At an alpha level of .05, can we conclude that there has been a significant decrease in the meantime?
(Short Answer)
4.8/5  (34)
(34)
Determine the 95 percent confidence interval for the difference between two population means, where sample 1 has data: 16, 14, 19, 18, 19, 20, 15, 18, 17, 18; and sample 2 has data: 13, 19, 14, 17, 21, 14, 15, 10, 13, 15. (Assume equal population variances.)
(Short Answer)
4.9/5  (31)
(31)
When comparing the variances of two normally distributed populations using independent random samples, if s12 = s12, the calculated value of F will always be equal to one.
(True/False)
4.8/5  (24)
(24)
When we test H0: μ1 − μ2 ≤ 0, HA: μ1 − μ2 > 0, 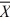 1 = 15.4,
1 = 15.4, 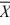 2 = 14.5, σ1 = 2, σ2 = 2.28,
n1 = 35, and n2 = 18 at α = .01, what is the value of the test statistic?
2 = 14.5, σ1 = 2, σ2 = 2.28,
n1 = 35, and n2 = 18 at α = .01, what is the value of the test statistic?
(Short Answer)
4.8/5  (39)
(39)
Calculate the t statistic for testing equality of means where 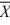 1 = 8.2,
1 = 8.2, 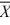 2 = 11.3, s12 = 5.4,
s22 = 5.2, n1 = 6, and n2 = 7. (Assume equal population variances.)
2 = 11.3, s12 = 5.4,
s22 = 5.2, n1 = 6, and n2 = 7. (Assume equal population variances.)
(Short Answer)
4.8/5  (33)
(33)
When we are testing a hypothesis about the difference in two population proportions based on large independent samples, we compute a combined (pooled) proportion from the two samples if we assume that there is no difference between the two proportions in our null hypothesis.
(True/False)
4.8/5  (42)
(42)
When comparing two independent population means, if n1 = 13 and n2 = 10, degrees of freedom for the t statistic is 22.
(True/False)
4.9/5  (33)
(33)
A test of mathematical ability is given to a random sample of 10 eighth-grade students before and after they complete a semester-long basic mathematics course. The mean score before the course was 119.60, and after the course the mean score was 130.80. The standard deviation of the difference is 16.061. Calculate a 99 percent confidence interval.
(Short Answer)
4.8/5  (30)
(30)
The registrar at a state college is interested in determining whether there is a difference of more than one credit hour between male and female students in the average number of credit hours taken during a term. She selected a random sample of 60 male and 60 female students and observed the following sample information.
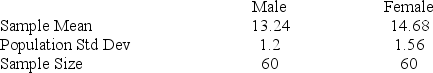 Set up the alternative hypothesis to test the claim.
Set up the alternative hypothesis to test the claim.
(Short Answer)
4.8/5  (34)
(34)
Using a 90 percent confidence interval of [−.0076, .0276] for the difference between the proportions of failures in factory 1 and factory 2, where ![Using a 90 percent confidence interval of [−.0076, .0276] for the difference between the proportions of failures in factory 1 and factory 2, where = 05, = .24, n<sub>1</sub> = 500, and n<sub>2</sub> = 2000, can we reject the null hypothesis at α = .10?](https://storage.examlex.com/TB7056/11ead627_0a6a_04a5_93a1_a51f84bf3e94_TB7056_11.jpg) = 05,
= 05, ![Using a 90 percent confidence interval of [−.0076, .0276] for the difference between the proportions of failures in factory 1 and factory 2, where = 05, = .24, n<sub>1</sub> = 500, and n<sub>2</sub> = 2000, can we reject the null hypothesis at α = .10?](https://storage.examlex.com/TB7056/11ead627_0a6a_04a6_93a1_5172b9fa233e_TB7056_11.jpg) = .24, n1 = 500, and
n2 = 2000, can we reject the null hypothesis at α = .10?
= .24, n1 = 500, and
n2 = 2000, can we reject the null hypothesis at α = .10?
(Short Answer)
4.8/5  (32)
(32)
Showing 121 - 140 of 140
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)