Exam 11: Statistical Inferences Based on Two Samples

A coffee shop franchise owner is looking at two possible locations for a new shop. To help him decide, he looks at the number of pedestrians that go by each of the two locations in one-hour segments. At location A, counts are taken for 35 one-hour units, with a mean number of pedestrians of 421 and a sample standard deviation of 122. At the second location (B), counts are taken for 50 one-hour units, with a mean number of pedestrians of 347 and a sample standard deviation of 85. Assume the two population variances are not known but are equal. Calculate a 95 percent confidence interval for the difference in pedestrian traffic at the two locations.

Suppose that a realtor is interested in comparing the price of midrange homes in two cities in a midwestern state. She conducts a small survey in the two cities, looking at the price of midrange homes. Assume equal population variances. Set up the alternative hypothesis to test the claim that there is a difference in the mean price of midrange homes of the two cities.

What is the value of the F statistic for H₀: σ₁² ≤ σ₁², H_A: σ₁² > σ₁², where s₁ = 3.3 and s₂ = 2.1?

In testing the difference between two independent population means, if the assumption is of unequal variances, the critical value of the t statistic is obtained by calculating the ________.

When testing H₀: σ₁² = σ₁², H_A: σ₁² > σ₂² at α = .01, where n₁ = 5, n₂ = 6, s₁² = 15,750, and s₂² = 10,920, what critical value do we use?

When testing the difference for the population of paired differences in which two different observations are taken on the same units, the correct test statistic to use is ________.

In order to test the effectiveness of a drug called XZR designed to reduce cholesterol levels, the cholesterol levels of 9 heart patients are measured before they are given the drug. The same 9 patients use XZR for two continuous months. After two months of continuous use, the cholesterol levels are measured again. The comparison of cholesterol levels before versus after administering the drug is an example of testing the difference between

When testing a hypothesis about the mean of a population of paired differences in which two different observations are taken on the same units, the correct test statistic to use is ________.

An experiment in which there is no relationship between the measurements on the different samples is a(n) ________ experiment.

In testing the difference between the means of two normally distributed populations using independent random samples with equal variances, the correct test statistic to use is the

Testing H₀: σ₁² ≤ σ₂², H_A: σ₁² > σ₂² at α = .05, where n₁ = 16, n₂ = 19, s₁² = .03, and s₂² = .02, can we reject the null hypothesis?

When we test H₀: μ₁ − μ₂ ≤ 0, H_A: μ₁ − μ₂ > 0, 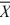₁ = 15.4, 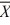₂ = 14.5, s₁ = 2, s₂ = 2.28, n₁ = 35, and n₂ = 18 at α = .01, can we reject the null hypothesis? (Assume unequal variances.)

A test of driving ability is given to a random sample of 10 student drivers before and after they complete a formal driver education course. Results follow. 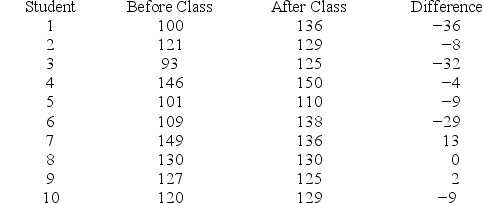Calculate the t statistic to test that there is no difference between the before-class scores and the after-class scores.

When we test H₀: μ₁ ≤ μ₂, H_A: μ₁ > μ₂ at α = .10, where 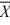₁ = 77.4, 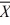₂ = 72.2, s₁ = 3.3, s₂ = 2.1, n₁ = 6, and n₂ = 6, can we reject the null hypothesis (using critical value rules)? (Assume equal variances.)

In an opinion survey, a random sample of 1,000 adults from the United States and 1,000 adults from Germany were asked whether they supported the death penalty. 590 American adults and 560 German adults indicated that they supported the death penalty. The researcher wants to know whether there is sufficient evidence to conclude that the proportion of adults who support the death penalty is higher in the United States than in Germany. What is the rejection point (critical value of the test statistic) at α = .05?

Given the following information about a hypothesis test of the difference between two means based on independent random samples, which one of the following is the correct rejection region at a significance level of .05? H_A: μ_A > μ_B, 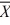₁ = 12, 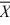₂ = 9, s₁ = 4, s₂ = 2, n₁ = 13, n₂ = 10.

In order to test the effectiveness of a drug called XZR designed to reduce cholesterol levels, the cholesterol levels of 9 heart patients are measured before they are given the drug. The same 9 patients use XZR for two continuous months. After two months of continuous use, the cholesterol levels are measured again. The comparison of cholesterol levels before versus after the administration of the drug is an example of testing the difference between two ________.

When comparing two independent population variances, the correct test statistic to use is ________.

In testing the difference between the means of two independent populations, the variances of the two samples can be pooled if the population variances are assumed to ________.

A test of mathematical ability is given to a random sample of 10 eighth-grade students before and after they complete a semester-long basic mathematics course. The mean score before the course was 119.60, and after the course the mean score was 130.80. The standard deviation of the difference is 16.061. Test the hypothesis that scores were higher after the course at = .05 using a t test.