Construct a 95 percent confidence interval for μ1 − μ2, where 1 = 34.36, 2 = 26.45, s1 = 9, s2 = 6, n1 = 10, n2 = 16. (Assume equal population variances.)

[1.86, 13.96] t 24,05 = 2.064 S 2 = @#IMG-DLM& =

Find a 95 percent confidence interval for μ1 − μ2, where n1 = 15, n2 = 10, 1 = 1.94, 2 = 1.04, s12 = .2025, and s22 = .0676. (Assume equal population variances.)

[0.573, 1.227] @#IMG-DLM& = @#IMG-DLM& =

Given two independent normal distributions with s12 − s22= 100, μ1 = μ2 = 50, and n1 = n2 = 50, the sampling distribution of the mean difference 1 − 2 will have a mean of ________.

A) 100 B) 1 C) 0 D) 50 E) 10 A) 100 B) 1 C) 0 D) 50 E) 10

Exam 11: Statistical Inferences Based on Two Samples

A new company is in the process of evaluating its customer service. The company offers two types of sales: (1) Internet sales and (2) store sales. The marketing research manager believes that the Internet sales are more than 10 percent higher than store sales. The alternative hypothesis for this problem would be stated as

(Multiple Choice)

4.9/5

(40)

Question 41

In testing the difference between the means of two independent populations, if neither population is normally distributed, then the sampling distribution of the difference in means will be approximately normal, provided that the sum of the sample sizes obtained from the two populations is at least 30.

(True/False)

4.8/5

(41)

Question 42

Coach Z, the mid-distance running coach for the Olympic team of an eastern European country, claims that his six-month training program significantly reduces the average time to complete a 1500-meter run. Five mid-distance runners were randomly selected. Their times (in minutes) for the 1500-meter run were recorded before and after six months of training under Coach Z. The results are given below. Construct the appropriate 95 percent confidence interval when we want to test whether there is a difference (s_d = .228).

(Short Answer)

4.9/5

(29)

Question 43

If we are testing the difference between the means of two normally distributed independent populations with samples of n₁ = 10, n₂ = 10, the degrees of freedom for the t statistic is ________.

(Multiple Choice)

4.8/5

(34)

Question 44

In an experiment involving matched pairs, a sample of 12 pairs of observations is collected. The degrees of freedom for the t statistic is 10.

(True/False)

4.9/5

(37)

Question 45

Testing H₀: σ₁² = σ₁², H_A: σ₁² > σ₂² at α = .01, where n₁ = 5, n₂ = 6, s₁² = 15,750, and s₂² = 10,920, can we reject the null hypothesis?

(Short Answer)

4.9/5

(38)

Question 46

Construct a 95 percent confidence interval for μ₁ − μ₂, where 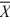₁ = 34.36, 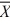₂= 26.45, s₁ = 9, s₂ = 6, n₁ = 10, n₂ = 16. (Assume equal population variances.)

(Short Answer)

4.8/5

(33)

Question 47

Given the following information about a hypothesis test of the difference between two means based on independent random samples, what is the standard deviation of the difference between the two means? Assume that the samples are obtained from normally distributed populations having equal variances. H_A: μ_A > μ_B, 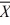₁ = 12, 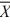₂ = 9, s₁ = 5, s₂ = 3, n₁ = 13, n₂ = 10.

(Multiple Choice)

4.9/5

(33)

Question 48

A marketing research company surveyed grocery shoppers on the East Coast and West Coast to find the percentage of the customers who prefer chicken to other meat. The data are given below. The marketing research company is testing the hypothesis that the proportion of customers who prefer chicken is the same for the two regions. Test at α = .10.

(Short Answer)

4.8/5

(35)

Question 49

We are testing the hypothesis that the proportion of winter-quarter profit growth is more than 2 percent greater for consumer industry companies (CON) than for banking companies (BKG). At α = .10, given that 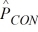= .20, 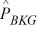= .14, n_CON = 300, and n_BKG = 400, can we reject the null hypothesis (using critical value rules)?

(Short Answer)

4.9/5

(35)

Question 50

A test of driving ability is given to a random sample of 10 student drivers before and after they complete a formal driver education course. Results follow. 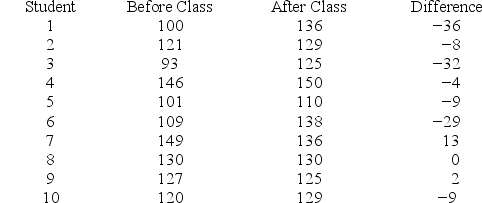Write the null and alternative hypotheses testing the claim that the test score is not affected by the course.

(Short Answer)

4.9/5

(39)

Question 51

Find a 95 percent confidence interval for μ₁ − μ₂, where n₁ = 15, n₂ = 10, 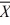₁ = 1.94, ₂ = 1.04, s₁² = .2025, and s₂² = .0676. (Assume equal population variances.)

(Short Answer)

4.7/5

(36)

Question 52

In an opinion survey, a random sample of 1,000 adults from the United States and 1,000 adults from Germany were asked whether they supported the death penalty. 590 American adults and 560 German adults indicated that they supported the death penalty. The researcher wants to know whether there is sufficient evidence to conclude that the proportion of adults who support the death penalty is higher in the United States than in Germany. What is the decision at α = .05?

(Short Answer)

4.9/5

(28)

Question 53

We use the following data for a test of the equality of variances for two populations at α = .10. Sample 1 is randomly selected from population 1 and sample 2 is randomly selected from population 2. Can we reject H₀ at α = .10?

(Short Answer)

5.0/5

(36)

Question 54

Find a 98 percent confidence interval for the paired difference d₁ − d₂ where 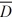= 1.6, S_d²= 40.96, n = 30

(Short Answer)

4.9/5

(31)

Question 55

When testing H₀: σ₁² ≤ σ₂² and H_A: σ₁² > σ₂², where s₁² = .004, s₂² = .002, n₁ = 4, and n₂ = 7 at α = .05, what critical value do we use?

(Short Answer)

4.7/5

(27)

Question 56

Given two independent normal distributions with s₁² − s₂²= 100, μ₁ = μ₂ = 50, and n₁ = n₂ = 50, the sampling distribution of the mean difference 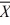₁ − 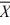₂ will have a mean of ________.

(Multiple Choice)

4.9/5

(39)

Question 57

In testing the difference between two population variances, it is a common practice to compute the F statistic so that its value is always greater than or equal to one.

(True/False)

4.8/5

(33)

Question 58

In general, the shape of the F distribution is ________.

(Multiple Choice)

5.0/5

(31)

Question 59

An independent samples experiment is an experiment in which there is no relationship between the measurements in the different samples.

(True/False)

4.8/5

(40)

Question 60

Showing 41 - 60 of 140

If we are testing the difference between the means of two normally distributed independent populations with samples of n₁ = 10, n₂ = 10, the degrees of freedom for the t statistic is ________.

In an experiment involving matched pairs, a sample of 12 pairs of observations is collected. The degrees of freedom for the t statistic is 10.

Testing H₀: σ₁² = σ₁², H_A: σ₁² > σ₂² at α = .01, where n₁ = 5, n₂ = 6, s₁² = 15,750, and s₂² = 10,920, can we reject the null hypothesis?

Construct a 95 percent confidence interval for μ₁ − μ₂, where ₁ = 34.36, ₂= 26.45, s₁ = 9, s₂ = 6, n₁ = 10, n₂ = 16. (Assume equal population variances.)

A test of driving ability is given to a random sample of 10 student drivers before and after they complete a formal driver education course. Results follow. Write the null and alternative hypotheses testing the claim that the test score is not affected by the course.

Find a 95 percent confidence interval for μ₁ − μ₂, where n₁ = 15, n₂ = 10, ₁ = 1.94, ₂ = 1.04, s₁² = .2025, and s₂² = .0676. (Assume equal population variances.)

We use the following data for a test of the equality of variances for two populations at α = .10. Sample 1 is randomly selected from population 1 and sample 2 is randomly selected from population 2. Can we reject H₀ at α = .10?

Find a 98 percent confidence interval for the paired difference d₁ − d₂ where = 1.6, S_d²= 40.96, n = 30

When testing H₀: σ₁² ≤ σ₂² and H_A: σ₁² > σ₂², where s₁² = .004, s₂² = .002, n₁ = 4, and n₂ = 7 at α = .05, what critical value do we use?

Given two independent normal distributions with s₁² − s₂²= 100, μ₁ = μ₂ = 50, and n₁ = n₂ = 50, the sampling distribution of the mean difference ₁ − ₂ will have a mean of ________.

In testing the difference between two population variances, it is a common practice to compute the F statistic so that its value is always greater than or equal to one.

In general, the shape of the F distribution is ________.

An independent samples experiment is an experiment in which there is no relationship between the measurements in the different samples.

An Introduction to Business Statistics and Analytics

Descriptive Statistics and Analytics: Tabular and Graphical Methods

Descriptive Statistics and Analytics: Numerical Methods

Probability and Probability Models

Predictive Analytics I: Trees, K-Nearest Neighbors, Naive Bayes,

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Confidence Intervals

Hypothesis Testing

Experimental Design and Analysis of Variance

Chi-Square Tests

Simple Linear Regression Analysis

Multiple Regression and Model Building

Predictive Analytics Ii: Logistic Regression, Discriminate Analysis,

Time Series Forecasting and Index Numbers

Nonparametric Methods

Decision Theory

Filters

Exam 11: Statistical Inferences Based on Two Samples

If we are testing the difference between the means of two normally distributed independent populations with samples of n1 = 10, n2 = 10, the degrees of freedom for the t statistic is ________.

In an experiment involving matched pairs, a sample of 12 pairs of observations is collected. The degrees of freedom for the t statistic is 10.

Testing H0: σ12 = σ12, HA: σ12 > σ22 at α = .01, where n1 = 5, n2 = 6, s12 = 15,750, and s22 = 10,920, can we reject the null hypothesis?

Construct a 95 percent confidence interval for μ1 − μ2, where 1 = 34.36, 2 = 26.45, s1 = 9, s2 = 6, n1 = 10, n2 = 16. (Assume equal population variances.)

A test of driving ability is given to a random sample of 10 student drivers before and after they complete a formal driver education course. Results follow. Write the null and alternative hypotheses testing the claim that the test score is not affected by the course.

Find a 95 percent confidence interval for μ1 − μ2, where n1 = 15, n2 = 10, 1 = 1.94, 2 = 1.04, s12 = .2025, and s22 = .0676. (Assume equal population variances.)

We use the following data for a test of the equality of variances for two populations at α = .10. Sample 1 is randomly selected from population 1 and sample 2 is randomly selected from population 2. Can we reject H0 at α = .10?

Find a 98 percent confidence interval for the paired difference d1 − d2 where = 1.6, Sd 2= 40.96, n = 30

When testing H0: σ12 ≤ σ22 and HA: σ12 > σ22, where s12 = .004, s22 = .002, n1 = 4, and n2 = 7 at α = .05, what critical value do we use?

Given two independent normal distributions with s12 − s22= 100, μ1 = μ2 = 50, and n1 = n2 = 50, the sampling distribution of the mean difference 1 − 2 will have a mean of ________.

In testing the difference between two population variances, it is a common practice to compute the F statistic so that its value is always greater than or equal to one.

In general, the shape of the F distribution is ________.

An independent samples experiment is an experiment in which there is no relationship between the measurements in the different samples.

An Introduction to Business Statistics and Analytics

Descriptive Statistics and Analytics: Tabular and Graphical Methods

Descriptive Statistics and Analytics: Numerical Methods

Probability and Probability Models

Predictive Analytics I: Trees, K-Nearest Neighbors, Naive Bayes,

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Confidence Intervals

Hypothesis Testing

Experimental Design and Analysis of Variance

Chi-Square Tests

Simple Linear Regression Analysis

Multiple Regression and Model Building

Predictive Analytics Ii: Logistic Regression, Discriminate Analysis,

Time Series Forecasting and Index Numbers

Nonparametric Methods

Decision Theory

Filters

If we are testing the difference between the means of two normally distributed independent populations with samples of n₁ = 10, n₂ = 10, the degrees of freedom for the t statistic is ________.

Testing H₀: σ₁² = σ₁², H_A: σ₁² > σ₂² at α = .01, where n₁ = 5, n₂ = 6, s₁² = 15,750, and s₂² = 10,920, can we reject the null hypothesis?

Construct a 95 percent confidence interval for μ₁ − μ₂, where ₁ = 34.36, ₂= 26.45, s₁ = 9, s₂ = 6, n₁ = 10, n₂ = 16. (Assume equal population variances.)

Find a 95 percent confidence interval for μ₁ − μ₂, where n₁ = 15, n₂ = 10, ₁ = 1.94, ₂ = 1.04, s₁² = .2025, and s₂² = .0676. (Assume equal population variances.)

We use the following data for a test of the equality of variances for two populations at α = .10. Sample 1 is randomly selected from population 1 and sample 2 is randomly selected from population 2. Can we reject H₀ at α = .10?

Find a 98 percent confidence interval for the paired difference d₁ − d₂ where = 1.6, S_d²= 40.96, n = 30

When testing H₀: σ₁² ≤ σ₂² and H_A: σ₁² > σ₂², where s₁² = .004, s₂² = .002, n₁ = 4, and n₂ = 7 at α = .05, what critical value do we use?

Given two independent normal distributions with s₁² − s₂²= 100, μ₁ = μ₂ = 50, and n₁ = n₂ = 50, the sampling distribution of the mean difference ₁ − ₂ will have a mean of ________.