Exam 4: Probability and Probability Distributions
Exam 1: Introduction to Business Analytics29 Questions
Exam 2: Describing the Distribution of a Single Variable100 Questions
Exam 3: Finding Relationships Among Variables85 Questions
Exam 4: Probability and Probability Distributions114 Questions
Exam 5: Normal, Binomial, Poisson, and Exponential Distributions125 Questions
Exam 6: Decision Making Under Uncertainty107 Questions
Exam 7: Sampling and Sampling Distributions90 Questions
Exam 8: Confidence Interval Estimation84 Questions
Exam 9: Hypothesis Testing87 Questions
Exam 10: Regression Analysis: Estimating Relationships92 Questions
Exam 11: Regression Analysis: Statistical Inference82 Questions
Exam 12: Time Series Analysis and Forecasting106 Questions
Exam 13: Introduction to Optimization Modeling97 Questions
Exam 14: Optimization Models114 Questions
Exam 15: Introduction to Simulation Modeling82 Questions
Exam 16: Simulation Models102 Questions
Exam 17: Data Mining20 Questions
Exam 18: Importing Data Into Excel19 Questions
Exam 19: Analysis of Variance and Experimental Design20 Questions
Exam 20: Statistical Process Control20 Questions
Select questions type
The number of car insurance policy holders is an example of a discrete random variable.
(True/False)
4.7/5  (34)
(34)
What is the probability of observing the sale of no more than two bats on a given day at this sporting goods store?
(Short Answer)
4.9/5  (33)
(33)
If two events are mutually exclusive, what is the probability that one or the other occurs?
(Multiple Choice)
4.9/5  (30)
(30)
If events A and B have nonzero probabilities, then they can be both independent and mutually exclusive.
(True/False)
4.8/5  (29)
(29)
Suppose a randomly selected patron is a female. What is the probability that the patron prefers wine?
(Short Answer)
4.8/5  (28)
(28)
The probabilities shown in a table with two rows, 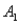 and
and 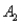 and two columns,
and two columns, 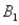 and
and 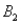 , are as follows: P(
, are as follows: P( 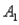 and
and 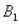 ) = .10, P(
) = .10, P( 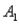 and
and 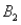 ) = .30, P(
) = .30, P( 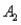 and
and 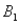 ) = .05, and P(
) = .05, and P( 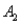 and
and 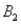 ) = .55. Then P(
) = .55. Then P( 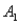 |
| 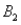 ), calculated up to two decimals, is:
), calculated up to two decimals, is:
(Multiple Choice)
4.7/5  (28)
(28)
Suppose that after graduation, you will either buy a new car (event A) or take a trip to Europe (event B). In this case, events A and B are mutually exclusive.
(True/False)
4.9/5  (44)
(44)
If A and B are any two events with P(A) = .8 and P(B|A) = .4, then the joint probability of A and B is:
(Multiple Choice)
4.9/5  (41)
(41)
Two or more events are said to be mutually exclusive if at most one of them can occur.
(True/False)
4.9/5  (35)
(35)
A sporting goods store sells softball bats. Let X be the numbers of bats sold on a typical day at the store. Based on the store historical data, the probability distribution of X is provided in the table below.
Sales (in units)  -What is the expected number of bats sold on a typical day?
-What is the expected number of bats sold on a typical day?
(Short Answer)
4.8/5  (30)
(30)
Two or more events are said to be exhaustive if one of them must occur.
(True/False)
4.8/5  (39)
(39)
What is the probability that a respondent chosen at random is a female and does not enjoy shopping for clothing?
(Essay)
4.9/5  (33)
(33)
What is probability of observing the sale of no more than 1 bat at this sporting goods store?
(Short Answer)
4.9/5  (35)
(35)
If two events are collectively exhaustive, what is the probability that both occur at the same time?
(Multiple Choice)
4.9/5  (35)
(35)
Showing 41 - 60 of 114
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)