Chat with AIExam 13: Introduction to Optimization Modeling
A feasible solution does not have to satisfy any constraints as long as it is logical.
(34) 
VerifiedFalse
Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant, which produces 5000 tons per month, and the Lakeview plant, which can produce 7000 tons per month. Sinclair sells its polyethylene to three different GM auto plants: Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below: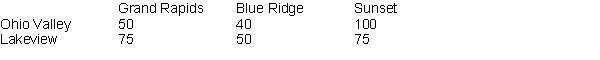 
-What are the constraints in this problem?
-What are the constraints in this problem? (31) Verifiedx11 + x12+ x13 = 5000 (Ohio Valley supply)
x21+ x22+ x23 = 7000 (Lakeview supply)
x11 + x21 = 3000 (Grand Rapids demand)
x12+ x22 = 5000 (Blue Ridge demand)
x13+ x23 = 4000 (Sunset demand)
(A) Find an optimal solution to the problem. What is the production plan, and what is the total revenue?
(B) Obtain a sensitivity report for the solution reported in (A). Which constraints are binding?
(C) What is the incremental contribution associated with adding an hour of assembly time? Over what range of increase is the marginal value valid?
(D) What is the value of additional capacity on the polisher? How much increase and decrease in this capacity is possible before a change occurs in the optimal production schedule?
(E) An advertising agency has devised a marketing plan for the Western Chassis Company that will increase the market for Deluxe chassis. The plan will increase demand by 75 Deluxe chassis per month at a cost of $100 per month. Should Western adopt the plan? Briefly explain why.
(F) Suppose that four more hours of chassis assembly time could be made available. How much would profit change?
(G) Suppose next that Western's marketing department proposes lowering the price for a standard chassis from $12 to $11.50 so that more can be sold (since there is slack under the demand constraint). Would the optimal solution change? Explain why, or why not.
(H) If Western could obtain 1,000 pounds more of raw material (steel or aluminum), which should it procure? How much should they be willing to pay per pound for the steel or aluminum? Explain your answer.
(I) In doing some contingency planning, Western thinks that the aging stamping machine will soon need to be taken down for repairs that could last 2 months and will cost $10,000. During that time, they can continue to operate by outsourcing the stamping at $2.50 per chassis (deluxe or standard), although the capacity will be reduced from 2,500 to 1,500. What will be the total cost to repair the stamping machine?
(26) Verified(A)
SS = pounds of steel sheeting produced and sold = 1000
AS = pounds of aluminum sheeting produced and sold = 2000
SC = number of Standard chassis racks produced and sold = 800
DC = number of Deluxe chassis racks produced and sold = 1000
Profit = $26,200
(B)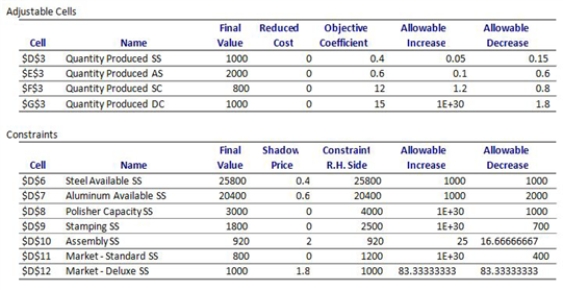 
Steel available, Aluminum available, Assembly SS, and Market Deluxe SS all have nonzero shadow prices, so they are binding.
(C) Incremental contribution is $2 per hour, with an allowable increase of 25 hours.
(D) The value of additional capacity on the polisher is zero, since it is not binding. The allowable increase is unbounded, and the allowable decrease is 1000.
(E) The change in the profit would be $1.8/hour shadow price times 75 hours, or $135, so Western should adopt the plan.
(F) Profit would increase by $8 (4 hours times $2/hour shadow price)
(G) The optimal solution would not change, because the change in the objective coefficient is within the allowable decrease (-$0.8). Note that since this would not result in any more standard chassis being sold, profit would decrease by $400.
(H) They should procure 1,000 pounds more of aluminum, since the shadow price is higher than that for steel (0.6 vs. 0.4). This results in additional profit of $600.
(I) The total cost will be the sum of the repairs ($10,000), the outsourcing cost ($2.50 per chassis, extended by how many chassis will be produced) and any reduction in profit due to the restricted stamping capacity. Note that since the capacity reduction on stamping is greater than the allowable decrease, a new production plan will be required. This new plan (0 SS, 4,000 AS, 500 SC, 1,000 DC) results in profit of $23,400, which is a reduction of $2,800 from the existing optimal profit of $26,200. With the production plan determined, the outsourcing cost can be determined (500 SC + 1000 DC = 1500 * $2.50 = $3,750). Thus the total cost will be $10,000 + 2 months*($2,800 + $3,750) = $23,100.
An efficient algorithm for finding the optimal solution in a linear programming model is the:
(25) Consider the following linear programming problem: Maximize: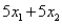 
Subject to: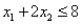 
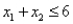
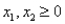The above linear programming problem:
Subject to: The above linear programming problem: (36) When formulating a linear programming spreadsheet model, there is one target (objective) cell that contains the value of the objective function.
(39) Write out an algebraic expression for the objective function in this problem.
(34) The prototype linear programming problem is to select an optimal mix of products to produce to maximize profit. This type of problem is referred to as the:
(46) Shadow prices are associated with nonbinding constraints, and show the change in the optimal objective function value when the right side of the constraint equation changes by one unit.
(34) The feasible region in all linear programming problems is bounded by:
(35) When using the graphical solution method to solve linear programming problems, the set of points that satisfy all constraints is called the:
(36) The most important solution method for linear programming problems is known as the:
(36) (A) Write out algebraic expressions for all of the constraints in this problem.
(B) Construct a graph of the feasible region for this problem, given the constraints you identified in (A).
(C) Describe how you would find the location of the optimal solution in the feasible region you graphed in (B).
(D) Use the procedure you described in (C) to identify the optimal production plan. Confirm your solution using Solver. What is the maximized profit?
(E) What constraints are binding on the optimal solution? Use your graphical solution to explain your answer.
(39) (A) Determine how to minimize the total cost of meeting the next 3 quarters' demand. Assume that 1000 usable units are available at the beginning of quarter 1.
(B) Referring to (A), the company wants to know how much money it would be worth to decrease the percentage of unsuitable items and/or the percentage of items that spoil. Write a short report that provides relevant information. Base your report on two uses of the SolverTable add-in: one where the percentage of unsuitable items decreases and the percentage of items that spoil stays at 10%; and one where the percentage of unsuitable items stays at 20% and the percentage of items that spoil decreases.
(36) A linear programming problem with _____decision variable(s) can be solved by a graphical solution method.
(40) The optimal solution to any linear programming model is the:
(39) A decision support system is a user-friendly system where an end user can enter inputs to a model and see outputs, but need not be concerned with technical details.
(33) Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant, which produces 5000 tons per month, and the Lakeview plant, which can produce 7000 tons per month. Sinclair sells its polyethylene to three different GM auto plants: Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below: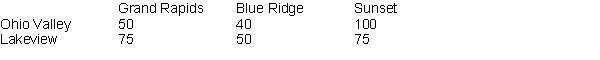
-What is the optimal shipping plan? What are the total costs in that case?
-What is the optimal shipping plan? What are the total costs in that case? (36) A 12-month rolling planning horizon is a single model where the decision in the first period is implemented.
(43) 
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)