Question 1

To perform sensitivity analysis involving an integer linear program, it is recommended to

Accepted Answer

A)  use the dual prices very cautiously. 
B)  make multiple computer runs. 
C)  use the same approach as you would for a linear program. 
D)  use LP relaxation. 
A)  use the dual prices very cautiously. 
B)  make multiple computer runs. 
C)  use the same approach as you would for a linear program. 
D)  use LP relaxation.

Question 2

Simplon Manufacturing must decide on the processes to use to produce 1650 units. If machine 1 is used, its production will be between 300 and 1500 units. Machine 2 and/or machine 3 can be used only if machine 1's production is at least 1000 units. Machine 4 can be used with no restrictions.   ​
(HINT: Use an additional 0 - 1 variable to indicate when machines 2 and 3 can be used.)

Accepted Answer

Let U_i = the number of units made by ma

Question 3

Modeling a fixed cost problem as an integer linear program requires

Accepted Answer

A)  adding the fixed costs to the corresponding variable costs in the objective function. 
B)  using 0-1 variables. 
C)  using multiple-choice constraints. 
D)  using LP relaxation. 
A)  adding the fixed costs to the corresponding variable costs in the objective function. 
B)  using 0-1 variables. 
C)  using multiple-choice constraints. 
D)  using LP relaxation.

Question 4

If Project 5 must be completed before Project 6, the constraint would be x5 − x6 ≤ 0.

Accepted Answer

A) True 
 B)False

Question 5

In a model, x1 ≥ 0 and integer, x2 ≥ 0, and x3 = 0, 1. Which solution would not be feasible?

Accepted Answer

A)  x1 = 5, x2 = 3, x3 = 0 
B)  x1 = 4, x2 = .389, x3 = 1 
C)  x1 = 2, x2 = 3, x3 = .578 
D)  x1 = 0, x2 = 8, x3 = 0 
A)  x1 = 5, x2 = 3, x3 = 0 
B)  x1 = 4, x2 = .389, x3 = 1 
C)  x1 = 2, x2 = 3, x3 = .578 
D)  x1 = 0, x2 = 8, x3 = 0

Question 6

Consider a capital budgeting example with five projects from which to select. Let xi = 1 if project i is selected, 0 if not, for i = 1,...,5. Write the appropriate constraint(s) for each condition. Conditions are independent.
a.Choose no fewer than three projects.
b.If project 3 is chosen, project 4 must be chosen.
c.If project 1 is chosen, project 5 must not be chosen.
d.Projects cost 100, 200, 150, 75, and 300 respectively. The budget is 450.
e.No more than two of projects 1, 2, and 3 can be chosen.

Accepted Answer

a.x₁ + x₂ + x₃ + x₄ + x₅ ≥ 3 B.x₃ −

Question 7

constraints involve binary variables.

Accepted Answer

A) True 
 B)False

Question 8

Let x1 and x2 be 0 - 1 variables whose values indicate whether projects 1 and 2 are not done or are done. Which answer below indicates that project 2 can be done only if project 1 is done?

Accepted Answer

A)  x1 + x2 = 1 
B)  x1 + x2 = 2 
C)  x1 − x2 ≤ 0 
D)  x1 − x2 ≥ 0 
A)  x1 + x2 = 1 
B)  x1 + x2 = 2 
C)  x1 − x2 ≤ 0 
D)  x1 − x2 ≥ 0

Question 9

Market Pulse Research has conducted a study for Lucas Furniture on some designs for a new commercial office desk. Three attributes were found to be most influential in determining which desk is most desirable: number of file drawers, the presence or absence of pullout writing boards, and simulated wood or solid color finish. Listed below are the part-worths for each level of each attribute provided by a sample of 7 potential Lucas customers.
​​   ​
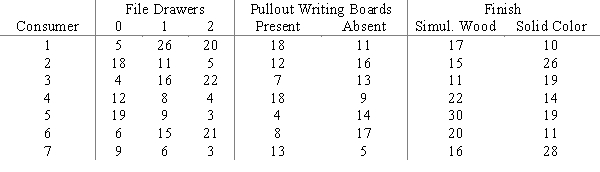
Suppose the overall utility (sum of part-worths) of the current favorite commercial office desk is 50 for each customer. What is the product design that will maximize the share of choices for the seven sample participants? Formulate and solve, using Lindo or Excel, this 0 - 1 integer programming problem.

Accepted Answer

Solution:
Lucas should choose these prod

Question 10

Hansen Controls has been awarded a contract for a large number of control panels. To meet this demand, it will use its existing plants in San Diego and Houston, and consider new plants in Tulsa, St. Louis, and Portland. Finished control panels are to be shipped to Seattle, Denver, and Kansas City. Pertinent information is given in the table.
​   ​
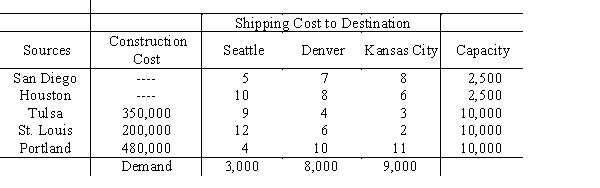
Develop a model whose solution would reveal which plants to build and the optimal shipping schedule.

Accepted Answer

Let P_ij = the number of panels shipped fro

Question 11

Solve the following problem graphically.
Min
6X + 11Y
s.t.
9X + 3Y ≥ 27
7X + 6Y ≥ 42
4X + 8Y ≥ 32
X, Y ≥ 0 and integer
​
a.Graph the constraints for this problem. Indicate all feasible solutions.
b.Find the optimal solution to the LP Relaxation. Round up to find a feasible integer solution. Is this solution optimal?
c.Find the optimal solution.

Accepted Answer

a.The feasible region is the set of inte

Question 12

Slack and surplus variables are not useful in integer linear programs.

Accepted Answer

A) True 
 B)False

Question 13

Some linear programming problems have a special structure that guarantees the variables will have integer values.

Accepted Answer

A) True 
 B)False

Question 14

​Integer linear programs are harder to solve than linear programs.

Accepted Answer

A) True 
 B)False

Question 15

The solution to the LP Relaxation of a minimization problem will always be less than or equal to the value of the integer program minimization problem.

Accepted Answer

A) True 
 B)False

Question 16

If the acceptance of project A is conditional on the acceptance of project B, and vice versa, the appropriate constraint to use is a

Accepted Answer

A)  multiple-choice constraint. 
B)  k out of n alternatives constraint. 
C)  mutually exclusive constraint. 
D)  corequisite constraint. 
A)  multiple-choice constraint. 
B)  k out of n alternatives constraint. 
C)  mutually exclusive constraint. 
D)  corequisite constraint.

Question 17

​Most practical applications of integer linear programming involve only 0 -1 integer variables.

Accepted Answer

A) True 
 B)False

Question 18

A constraint involves selecting k out of n alternatives, where k ≥ 2.

Accepted Answer

A) True 
 B)False

Question 19

​List and explain four types of constraints involving 0-1 integer variables only.

Accepted Answer

1. Binary Constraints: These constraints

Question 20

The LP Relaxation contains the objective function and constraints of the IP problem, but drops all integer restrictions.

Accepted Answer

A) True 
 B)False

To perform sensitivity analysis involving an integer linear program, it is recommended to

Modeling a fixed cost problem as an integer linear program requires

If Project 5 must be completed before Project 6, the constraint would be x₅ − x₆ ≤ 0.

In a model, x₁ ≥ 0 and integer, x₂ ≥ 0, and x₃ = 0, 1. Which solution would not be feasible?

constraints involve binary variables.

Let x₁ and x₂ be 0 - 1 variables whose values indicate whether projects 1 and 2 are not done or are done. Which answer below indicates that project 2 can be done only if project 1 is done?

Slack and surplus variables are not useful in integer linear programs.

Some linear programming problems have a special structure that guarantees the variables will have integer values.

Integer linear programs are harder to solve than linear programs.

The solution to the LP Relaxation of a minimization problem will always be less than or equal to the value of the integer program minimization problem.

If the acceptance of project A is conditional on the acceptance of project B, and vice versa, the appropriate constraint to use is a

Most practical applications of integer linear programming involve only 0 -1 integer variables.

A constraint involves selecting k out of n alternatives, where k ≥ 2.

List and explain four types of constraints involving 0-1 integer variables only.

The LP Relaxation contains the objective function and constraints of the IP problem, but drops all integer restrictions.

Introduction

An Introduction to Linear Programming

Linear Programming: Sensitivity Analysis and Interpretation of Solution

Linear Programming Applications in Marketing, Finance, and Operations Management

Advanced Linear Programming Applications

Distribution and Network Models

Nonlinear Optimization Models

Project Scheduling: Pertcpm

Inventory Models

Waiting Line Models

Simulation

Decision Analysis

Multicriteria Decisions

Time Series Analysis and Forecasting

Markov Processes

Linear Programming: Simplex Method

Simplex-Based Sensitivity Analysis and Duality

Solution Procedures for Transportation and Assignment Problems

Minimal Spanning Tree

Dynamic Programming

Filters

Exam 7: Integer Linear Programming

To perform sensitivity analysis involving an integer linear program, it is recommended to

Modeling a fixed cost problem as an integer linear program requires

If Project 5 must be completed before Project 6, the constraint would be x5 − x6 ≤ 0.

In a model, x1 ≥ 0 and integer, x2 ≥ 0, and x3 = 0, 1. Which solution would not be feasible?

constraints involve binary variables.

Let x1 and x2 be 0 - 1 variables whose values indicate whether projects 1 and 2 are not done or are done. Which answer below indicates that project 2 can be done only if project 1 is done?

Slack and surplus variables are not useful in integer linear programs.

Some linear programming problems have a special structure that guarantees the variables will have integer values.

​Integer linear programs are harder to solve than linear programs.

The solution to the LP Relaxation of a minimization problem will always be less than or equal to the value of the integer program minimization problem.

If the acceptance of project A is conditional on the acceptance of project B, and vice versa, the appropriate constraint to use is a

​Most practical applications of integer linear programming involve only 0 -1 integer variables.

A constraint involves selecting k out of n alternatives, where k ≥ 2.

​List and explain four types of constraints involving 0-1 integer variables only.

The LP Relaxation contains the objective function and constraints of the IP problem, but drops all integer restrictions.

Introduction

An Introduction to Linear Programming

Linear Programming: Sensitivity Analysis and Interpretation of Solution

Linear Programming Applications in Marketing, Finance, and Operations Management

Advanced Linear Programming Applications

Distribution and Network Models

Nonlinear Optimization Models

Project Scheduling: Pertcpm

Inventory Models

Waiting Line Models

Simulation

Decision Analysis

Multicriteria Decisions

Time Series Analysis and Forecasting

Markov Processes

Linear Programming: Simplex Method

Simplex-Based Sensitivity Analysis and Duality

Solution Procedures for Transportation and Assignment Problems

Minimal Spanning Tree

Dynamic Programming

Filters

If Project 5 must be completed before Project 6, the constraint would be x₅ − x₆ ≤ 0.

In a model, x₁ ≥ 0 and integer, x₂ ≥ 0, and x₃ = 0, 1. Which solution would not be feasible?

Let x₁ and x₂ be 0 - 1 variables whose values indicate whether projects 1 and 2 are not done or are done. Which answer below indicates that project 2 can be done only if project 1 is done?

Integer linear programs are harder to solve than linear programs.

Most practical applications of integer linear programming involve only 0 -1 integer variables.

List and explain four types of constraints involving 0-1 integer variables only.