Exam 7: Integer Linear Programming
Exam 1: Introduction63 Questions
Exam 2: An Introduction to Linear Programming66 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution56 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management63 Questions
Exam 5: Advanced Linear Programming Applications46 Questions
Exam 6: Distribution and Network Models70 Questions
Exam 7: Integer Linear Programming61 Questions
Exam 8: Nonlinear Optimization Models51 Questions
Exam 9: Project Scheduling: Pertcpm59 Questions
Exam 10: Inventory Models65 Questions
Exam 11: Waiting Line Models68 Questions
Exam 12: Simulation62 Questions
Exam 13: Decision Analysis97 Questions
Exam 14: Multicriteria Decisions50 Questions
Exam 15: Time Series Analysis and Forecasting63 Questions
Exam 16: Markov Processes49 Questions
Exam 17: Linear Programming: Simplex Method51 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality35 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems44 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming38 Questions
Select questions type
Your express package courier company is drawing up new zones for the location of drop boxes for customers. The city has been divided into the seven zones shown below. You have targeted six possible locations for drop boxes. The list of which drop boxes could be reached easily from each zone is listed below.  Let xi = 1 if drop box location i is used, 0 otherwise. Develop a model to provide the smallest number of locations yet make sure that each zone is covered by at least two boxes.
Let xi = 1 if drop box location i is used, 0 otherwise. Develop a model to provide the smallest number of locations yet make sure that each zone is covered by at least two boxes.
(Essay)
4.8/5  (40)
(40)
The solution to the LP Relaxation of a maximization integer linear program provides
(Multiple Choice)
4.9/5  (28)
(28)
Given the following all-integer linear program:
Max 15x1 + 2x2
s. t. 7x1 + x2 < 23
3x1 - x2 < 5
x1, x2 > 0 and integer
a. Solve the problem as an LP, ignoring the integer constraints.
b. What solution is obtained by rounding up fractions greater than or equal to 1/2? Is this the optimal integer solution?
c. What solution is obtained by rounding down all fractions? Is this the optimal integer solution? Explain.
d. Show that the optimal objective function value for the ILP is lower than that for the optimal LP.
e. Why is the optimal objective function value for the ILP problem always less than or equal to the corresponding LP's optimal objective function value? When would they be equal? Comment on the MILP's optimal objective function compared to the corresponding LP & ILP.
(Essay)
4.9/5  (40)
(40)
Most practical applications of integer linear programming involve
(Multiple Choice)
4.7/5  (30)
(30)
Which of the following applications modeled in the textbook does not involve only 0 - 1 integer variables?
(Multiple Choice)
4.9/5  (39)
(39)
Let x1 , x2 , and x3 be 0 - 1 variables whose values indicate whether the projects are not done (0) or are done (1). Which answer below indicates that at least two of the projects must be done?
(Multiple Choice)
4.9/5  (28)
(28)
The Westfall Company has a contract to produce 10,000 garden hoses for a large discount chain. Westfall has four different machines that can produce this kind of hose. Because these machines are from different manufacturers and use differing technologies, their specifications are not the same. 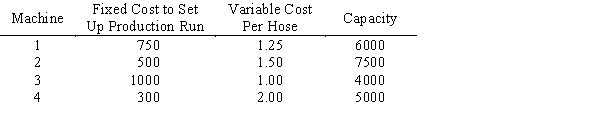
a.This problem requires two different kinds of decision variables. Clearly define each kind.
b.The company wants to minimize total cost. Give the objective function.
c.Give the constraints for the problem.
d.Write a constraint to ensure that if machine 4 is used, machine 1 cannot be.
a.This problem requires two different kinds of decision variables. Clearly define each kind.
b.The company wants to minimize total cost. Give the objective function.
c.Give the constraints for the problem.
d.Write a constraint to ensure that if machine 4 is used, machine 1 cannot be.
(Essay)
4.8/5  (31)
(31)
The use of integer variables creates additional restrictions but provides additional flexibility. Explain.
(Essay)
4.8/5  (39)
(39)
A business manager for a grain distributor is asked to decide how many containers of each of two grains to purchase to fill its 1,600 pound capacity warehouse. The table below summarizes the container size, availability, and expected profit per container upon distribution.

a. Formulate as a linear program with the decision variables representing the number of containers purchased of each grain. Solve for the optimal solution.
b. What would be the optimal solution if you were not allowed to purchase fractional containers?
c. There are three possible results from rounding an LP solution to obtain an integer solution:
(1) the rounded optimal LP solution will be the optimal IP solution;
(2) the rounded optimal LP solution gives a feasible, but not optimal IP solution;
(3) the rounded optimal LP solution is an infeasible IP solution.
For this problem (i) round down all fractions; (ii) round up all fractions; (iii) round off (to the nearest integer) all fractions (NOTE: Two of these are equivalent.) Which result above (1, 2, or 3) occurred under each rounding method?
a. Formulate as a linear program with the decision variables representing the number of containers purchased of each grain. Solve for the optimal solution.
b. What would be the optimal solution if you were not allowed to purchase fractional containers?
c. There are three possible results from rounding an LP solution to obtain an integer solution:
(1) the rounded optimal LP solution will be the optimal IP solution;
(2) the rounded optimal LP solution gives a feasible, but not optimal IP solution;
(3) the rounded optimal LP solution is an infeasible IP solution.
For this problem (i) round down all fractions; (ii) round up all fractions; (iii) round off (to the nearest integer) all fractions (NOTE: Two of these are equivalent.) Which result above (1, 2, or 3) occurred under each rounding method?
(Essay)
4.9/5  (38)
(38)
The constraint x1 − x2 = 0 implies that if project 1 is selected, project 2 cannot be.
(True/False)
4.7/5  (36)
(36)
The objective of the product design and market share optimization problem presented in the textbook is to choose the levels of each product attribute that will maximize the number of sampled customers preferring the brand in question.
(True/False)
4.9/5  (39)
(39)
Give a verbal interpretation of each of these constraints in the context of a capital budgeting problem.
a. x1 − x2 ≥ 0
b. x1 − x2 = 0
c. x1 + x2 + x3 ≤ 2
(Essay)
4.8/5  (34)
(34)
Explain how integer and 0-1 variables can be used in an objective function to minimize the sum of fixed and variable
costs for production on two machines.
(Essay)
4.9/5  (44)
(44)
Generally, the optimal solution to an integer linear program is less sensitive to the constraint coefficients than is a linear program.
(True/False)
4.8/5  (26)
(26)
Rounding the solution of an LP Relaxation to the nearest integer values provides
(Multiple Choice)
4.9/5  (33)
(33)
Assuming W1, W2 and W3 are 0 -1 integer variables, the constraint W1 + W2 + W3 < 1 is often called a
(Multiple Choice)
4.8/5  (34)
(34)
The constraint x1 + x2 + x3 + x4 ≤ 2 means that two out of the first four projects must be selected.
(True/False)
4.8/5  (29)
(29)
In a model involving fixed costs, the 0 - 1 variable guarantees that the capacity is not available unless the cost has been incurred.
(True/False)
4.8/5  (34)
(34)
The product design and market share optimization problem presented in the textbook is formulated as a 0-1 integer linear programming model.
(True/False)
4.7/5  (25)
(25)
Showing 21 - 40 of 61
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)