Question 1

Establish the identity.
-$$\cos ^ { 2 } x - \sin ^ { 2 } x = 1 - 2 \sin ^ { 2 } x$$

Accepted Answer

The answer of Establish the identity.
-\[\cos ^ { 2 }...

Question 2

Solve the problem using Snell's Law: $\frac { \sin \theta _ { 1 } } { \sin \theta _ { 2 } } = \frac { v _ { 1 } } { v _ { 2 } }$
-A light beam traveling through air makes an angle of incidence of 39° upon a second medium. The refracted beam makes an angle of refraction of 28°. What is the index of refraction of the material of the second medium?
Give the answer to two decimal places.

Accepted Answer

A)  0.47 
B)  0.75 
C)  0.63 
D)  1.34 
A)  0.47 
B)  0.75 
C)  0.63 
D)  1.34

Question 3

Find the exact value of the expression.
-$\cos \left( \frac { 5 \pi } { 18 } \right) \cos \left( \frac { 2 \pi } { 9 } \right) - \sin \left( \frac { 5 \pi } { 18 } \right) \sin \left( \frac { 2 \pi } { 9 } \right)$

Accepted Answer

A)  $- 1$ 
B)  1 
C)  0 
D)  $\frac { \sqrt { 2 } } { 2 }$ 
A)  $- 1$ 
B)  1 
C)  0 
D)  $\frac { \sqrt { 2 } } { 2 }$

Question 4

Solve the problem.
-Find $\sin \frac { \theta } { 2 }$, given that $\cos \theta = \frac { 1 } { 4 }$ and $\theta$ terminates in $0 < \theta < 90 ^ { \circ }$.

Accepted Answer

A)  $\frac { \sqrt { 8 + 2 \sqrt { 15 } } } { 4 }$ 
B)  $\frac { \sqrt { 6 } } { 4 }$ 
C)  $\frac { \sqrt { 8 - 2 \sqrt { 15 } } } { 4 }$ 
D)  $\frac { \sqrt { 10 } } { 4 }$ 
A)  $\frac { \sqrt { 8 + 2 \sqrt { 15 } } } { 4 }$ 
B)  $\frac { \sqrt { 6 } } { 4 }$ 
C)  $\frac { \sqrt { 8 - 2 \sqrt { 15 } } } { 4 }$ 
D)  $\frac { \sqrt { 10 } } { 4 }$

Question 5

Solve the problem.
-On a Touch-Tone phone, each button produces a unique sound. The sound produced is the sum of two tones, gi' $y = \sin ( 2 \pi l t )$ and $y = \sin ( 2 \pi h t )$
where $l$ and $h$ are the low and high frequencies (cycles per second) shown on the illustration.
 
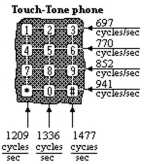 The sound produced is thus given by $$y = \sin ( 2 \pi l t ) + \sin ( 2 \pi h t )$$
Write the sound emitted by touching the 4 key as a product of sines and cosines.

Accepted Answer

A)  $y = 2 \sin ( 439 \pi t ) \cos ( 1,979 \pi t )$ 
B)  $y = 2 \sin ( 566 \pi t ) \cos ( 2,106 \pi t )$ 
C)  $y = 2 \sin ( 2,106 \pi t ) \cos ( 566 \pi t )$ 
D)  $y = 2 \sin ( 1,979 \pi t ) \cos ( 439 \pi t )$ 
A)  $y = 2 \sin ( 439 \pi t ) \cos ( 1,979 \pi t )$ 
B)  $y = 2 \sin ( 566 \pi t ) \cos ( 2,106 \pi t )$ 
C)  $y = 2 \sin ( 2,106 \pi t ) \cos ( 566 \pi t )$ 
D)  $y = 2 \sin ( 1,979 \pi t ) \cos ( 439 \pi t )$

Question 6

Complete the identity.
-$$\frac { \sin ^ { 2 } \theta - 1 } { \sin \theta + 1 } = ?$$

Accepted Answer

A)  $\sin \theta + 1$ 
B)  $\cos ^ { 2 } \theta$ 
C)  $\sin \theta - 1$ 
D)  $\sin \theta$ 
A)  $\sin \theta + 1$ 
B)  $\cos ^ { 2 } \theta$ 
C)  $\sin \theta - 1$ 
D)  $\sin \theta$

Question 7

Use a graphing utility to solve the equation on the interval 0 $0 ^ { \circ } \leq x < 360 ^ { \circ }$ . Express the solution(s) rounded to one decimal
place.
-$\cos ^ { 2 } x + \cos x - 1 = 0$

Accepted Answer

A)  103.2°, 145.2°, 283.2°, 325.2° 
B)  49.8°, 130.2°, 229.8°, 310.2° 
C)  51.8°, 308.2° 
D)  70.5°, 109.5°, 180.0° 
A)  103.2°, 145.2°, 283.2°, 325.2° 
B)  49.8°, 130.2°, 229.8°, 310.2° 
C)  51.8°, 308.2° 
D)  70.5°, 109.5°, 180.0°

Question 8

Find the domain of the function f and of its inverse function $\mathrm { f } ^ { - 1 }$ .
-$$f ( x ) = - 8 \cos ( 10 x + 4 )$$

Accepted Answer

A)  Domain of $\mathrm { f } : ( \infty , \infty )$
Domain of $\mathrm { f } ^ { - 1 } : ( \infty , \infty )$ 
B)  Domain of $f : ( \infty , \infty )$
Domain of $\mathrm { f } ^ { - 1 } : [ - 8,8 ]$ 
C)  Domain of $\mathrm { f } : [ - 8,8 ]$
Domain of $f ^ { - 1 } : ( \infty , \infty )$ 
D)  Domain of $\mathrm { f: } ( \infty , \infty )$

Domain of $f ^ { - 1 } : [ - 10,10 ]$ 
A)  Domain of $\mathrm { f } : ( \infty , \infty )$
Domain of $\mathrm { f } ^ { - 1 } : ( \infty , \infty )$ 
B)  Domain of $f : ( \infty , \infty )$
Domain of $\mathrm { f } ^ { - 1 } : [ - 8,8 ]$ 
C)  Domain of $\mathrm { f } : [ - 8,8 ]$
Domain of $f ^ { - 1 } : ( \infty , \infty )$ 
D)  Domain of $\mathrm { f: } ( \infty , \infty )$

Domain of $f ^ { - 1 } : [ - 10,10 ]$

Question 9

Establish the identity.
-$$\frac { 1 - 2 \sec x - 3 \sec ^ { 2 } x } { - \tan ^ { 2 } x } = \frac { 1 - 3 \sec x } { 1 - \sec x }$$

Accepted Answer

The answer of Establish the identity.
-\[\frac { 1 - 2...

Question 10

Find the exact value of the expression.
-$$\sin ^ { - 1 } \frac { \sqrt { 2 } } { 2 }$$

Accepted Answer

A)  $\frac { 3 \pi } { 4 }$ 
B)  $\frac { 2 \pi } { 3 }$ 
C)  $\frac { \pi } { 4 }$ 
D)  $\frac { \pi } { 3 }$ 
A)  $\frac { 3 \pi } { 4 }$ 
B)  $\frac { 2 \pi } { 3 }$ 
C)  $\frac { \pi } { 4 }$ 
D)  $\frac { \pi } { 3 }$

Question 11

Use the information given about the angle $$\theta , 0 \leq \theta \leq 2 \pi$$ , to find the exact value of the indicated trigonometric function.
-$\sin \theta = - \frac { 4 } { 5 } , \frac { 3 \pi } { 2 } < \theta < 2 \pi \quad$ Find $\cos ( 2 \theta ) .$

Accepted Answer

A)  $\frac { 24 } { 25 }$

В) $\frac { 7 } { 25 }$ 
C)  $- \frac { 7 } { 25 }$ 
D)  $- \frac { 24 } { 25 }$ 
A)  $\frac { 24 } { 25 }$

В) $\frac { 7 } { 25 }$ 
C)  $- \frac { 7 } { 25 }$ 
D)  $- \frac { 24 } { 25 }$

Question 12

Complete the identity.
-$$\frac { \sin \theta } { \cos \theta } + \frac { \cos \theta } { \sin \theta } = \text { ? }$$

Accepted Answer

A)  $- 2 \tan ^ { 2 } \theta$ 
B)  $\sec \theta \csc \theta$ 
C)  $\sin \theta \tan \theta$ 
D)  $1 + \cot \theta$ 
A)  $- 2 \tan ^ { 2 } \theta$ 
B)  $\sec \theta \csc \theta$ 
C)  $\sin \theta \tan \theta$ 
D)  $1 + \cot \theta$

Question 13

Solve the problem.
-You are flying a kite and want to know its angle of elevation. The string on the kite is 43 meters long and the
kite is level with the top of a building that you know is 28 meters high. Use an inverse trigonometric function to
find the angle of elevation of the kite. Round to two decimal places.

Accepted Answer

The answer of Solve the problem.
-You are flying a kite...

Question 14

Solve the problem.
-The two equal sides of an isosceles triangle measure three feet. Let the angle between the sides measure $\theta$. Find the area A of the triangle as a function of $\frac { \theta } { 2 }$. The answer may include more than one trigonometric function.

Accepted Answer

The answer of Solve the problem.
-The two equal sides of...

Question 15

Complete the identity.
-$$\sin \frac { \theta } { 2 } \cos \frac { \theta } { 2 } = ?$$

Accepted Answer

A)  $\frac { 1 } { 2 } \sin \theta$ 
B)  $\frac { 1 - \cos \theta } { 2 }$ 
C)  $\frac { 1 + \sin \theta } { 2 }$ 
D)  $\frac { 1 } { 2 } \cos \theta$ 
A)  $\frac { 1 } { 2 } \sin \theta$ 
B)  $\frac { 1 - \cos \theta } { 2 }$ 
C)  $\frac { 1 + \sin \theta } { 2 }$ 
D)  $\frac { 1 } { 2 } \cos \theta$

Question 16

Solve the problem.
-A product of two oscillations with different frequencies such as
$$f ( t ) = \sin ( 10 t ) \sin ( t )$$
is important in acoustics. The result is an oscillation with "oscillating amplitude."
(i) Writethe product $\mathrm { f } ( \mathrm { t } )$ of the two oscillations as a sum of two cosines and call it $g ( \mathrm { t } )$.
(ii) Usinga graphing utility, graph the function $g ( t )$ on the interval $0 \leq t \leq 2 \pi$.
(iii) On the same system as your graph, graph $y = \sin t$ and $y = - \sin t$.
(iv) Thelast two functions constitute an "envelope" for the function $g ( t )$. For certain values of $t$, the two cosine functions in $g ( t )$ cancel each other out and near-silence occurs; between these values, the two functions combine in varying degrees. The phenomenon is known (and heard) as "beats." For what values of $t$ do the functions cancel each other?

Accepted Answer

(i) @#LAT-DLM&
(ii),

Question 17

Solve the problem.
-Find $\tan \frac { \theta } { 2 }$, given that $\tan \theta = 3$ and $\theta$ terminates in $\pi < \theta < 3 \pi / 2$

Accepted Answer

A)  $\frac { \sqrt { 10 } - 1 } { - 3 }$ 
B)  $\frac { \sqrt { 10 } - 1 } { 3 }$ 
C)  $\frac { \sqrt { 10 } + 1 } { - 3 }$ 
D)  $\frac { \sqrt { 10 } + 1 } { 3 }$ 
A)  $\frac { \sqrt { 10 } - 1 } { - 3 }$ 
B)  $\frac { \sqrt { 10 } - 1 } { 3 }$ 
C)  $\frac { \sqrt { 10 } + 1 } { - 3 }$ 
D)  $\frac { \sqrt { 10 } + 1 } { 3 }$

Question 18

Find the exact value of the expression. Do not use a calculator.
-$\sin \left[ \sin ^ { - 1 } ( - 0.7 ) \right]$

Accepted Answer

A)  -0.7 
B)  -1.4286 
C)  -0.3 
D)  -1.5523 
A)  -0.7 
B)  -1.4286 
C)  -0.3 
D)  -1.5523

Question 19

Find the exact value under the given conditions.
-$\cos \alpha = - \frac { 5 } { 13 } , \frac { \pi } { 2 } < \alpha < \pi ; \quad \sin \beta = \frac { 8 } { 17 } , \frac { \pi } { 2 } < \alpha < \pi \quad$ Find $\tan ( \alpha - \beta )$.

Accepted Answer

A)  $\frac { 50 } { 19 }$

В) $\frac { 20 } { 3 }$ 
C)  $- \frac { 20 } { 3 }$ 
D)  $- \frac { 140 } { 171 }$ 
A)  $\frac { 50 } { 19 }$

В) $\frac { 20 } { 3 }$ 
C)  $- \frac { 20 } { 3 }$ 
D)  $- \frac { 140 } { 171 }$

Question 20

Find the exact value under the given conditions.
-$\sin \alpha = \frac { 20 } { 29 } , \frac { \pi } { 2 } < \alpha < \pi ; \quad \cos \beta = \frac { 3 } { 5 } , 0 < \beta < \frac { \pi } { 2 } \quad$ Find $\sin ( \alpha - \beta )$.

Accepted Answer

A)  $\frac { 143 } { 145 }$ 
B)  $- \frac { 17 } { 145 }$ 
C)  $\frac { 144 } { 145 }$ 
D)  $- \frac { 24 } { 145 }$ 
A)  $\frac { 143 } { 145 }$ 
B)  $- \frac { 17 } { 145 }$ 
C)  $\frac { 144 } { 145 }$ 
D)  $- \frac { 24 } { 145 }$

Establish the identity. - $\cos ^ { 2 } x - \sin ^ { 2 } x = 1 - 2 \sin ^ { 2 } x$

Find the exact value of the expression. - $\cos \left( \frac { 5 \pi } { 18 } \right) \cos \left( \frac { 2 \pi } { 9 } \right) - \sin \left( \frac { 5 \pi } { 18 } \right) \sin \left( \frac { 2 \pi } { 9 } \right)$

Solve the problem. -Find $\sin \frac { \theta } { 2 }$ , given that $\cos \theta = \frac { 1 } { 4 }$ and $\theta$ terminates in $0 < \theta < 90 ^ { \circ }$ .

Complete the identity. - $\frac { \sin ^ { 2 } \theta - 1 } { \sin \theta + 1 } = ?$

Use a graphing utility to solve the equation on the interval 0 $0 ^ { \circ } \leq x < 360 ^ { \circ }$ . Express the solution(s) rounded to one decimal place. - $\cos ^ { 2 } x + \cos x - 1 = 0$

Find the domain of the function f and of its inverse function $\mathrm { f } ^ { - 1 }$ . - $f ( x ) = - 8 \cos ( 10 x + 4 )$

Establish the identity. - $\frac { 1 - 2 \sec x - 3 \sec ^ { 2 } x } { - \tan ^ { 2 } x } = \frac { 1 - 3 \sec x } { 1 - \sec x }$

Find the exact value of the expression. - $\sin ^ { - 1 } \frac { \sqrt { 2 } } { 2 }$

Use the information given about the angle $\theta , 0 \leq \theta \leq 2 \pi$ , to find the exact value of the indicated trigonometric function. - $\sin \theta = - \frac { 4 } { 5 } , \frac { 3 \pi } { 2 } < \theta < 2 \pi \quad$ Find $\cos ( 2 \theta ) .$

Complete the identity. - $\frac { \sin \theta } { \cos \theta } + \frac { \cos \theta } { \sin \theta } = \text { ? }$

Solve the problem. -The two equal sides of an isosceles triangle measure three feet. Let the angle between the sides measure $\theta$ . Find the area A of the triangle as a function of $\frac { \theta } { 2 }$ . The answer may include more than one trigonometric function.

Complete the identity. - $\sin \frac { \theta } { 2 } \cos \frac { \theta } { 2 } = ?$

Solve the problem. -Find $\tan \frac { \theta } { 2 }$ , given that $\tan \theta = 3$ and $\theta$ terminates in $\pi < \theta < 3 \pi / 2$

Find the exact value of the expression. Do not use a calculator. - $\sin \left[ \sin ^ { - 1 } ( - 0.7 ) \right]$

Find the exact value under the given conditions. - $\cos \alpha = - \frac { 5 } { 13 } , \frac { \pi } { 2 } < \alpha < \pi ; \quad \sin \beta = \frac { 8 } { 17 } , \frac { \pi } { 2 } < \alpha < \pi \quad$ Find $\tan ( \alpha - \beta )$ .

Find the exact value under the given conditions. - $\sin \alpha = \frac { 20 } { 29 } , \frac { \pi } { 2 } < \alpha < \pi ; \quad \cos \beta = \frac { 3 } { 5 } , 0 < \beta < \frac { \pi } { 2 } \quad$ Find $\sin ( \alpha - \beta )$ .

Functions and Their Graphs

Linear and Quadratic Functions

Polynomial and Rational Functions

Exponential and Logarithmic Functions

Trigonometric Functions

Applications of Trigonometric Functions

Polar Coordinates; Vectors

Analytic Geometry

Systems of Equations and Inequalities

Sequences; Induction; the Binomial Theorem

Counting and Probability

A Preview of Calculus: the Limit, Derivative, and Integral of a Function

Review

Filters

Exam 6: Analytic Trigonometry

Establish the identity. - cos⁡2x−sin⁡2x=1−2sin⁡2x\cos ^ { 2 } x - \sin ^ { 2 } x = 1 - 2 \sin ^ { 2 } xcos2x−sin2x=1−2sin2x

Solve the problem. -Find sin⁡θ2\sin \frac { \theta } { 2 }sin2θ​ , given that cos⁡θ=14\cos \theta = \frac { 1 } { 4 }cosθ=41​ and θ\thetaθ terminates in 0<θ<90∘0 < \theta < 90 ^ { \circ }0<θ<90∘ .

Complete the identity. - sin⁡2θ−1sin⁡θ+1=?\frac { \sin ^ { 2 } \theta - 1 } { \sin \theta + 1 } = ?sinθ+1sin2θ−1​=?

Use a graphing utility to solve the equation on the interval 0 0∘≤x<360∘0 ^ { \circ } \leq x < 360 ^ { \circ }0∘≤x<360∘ . Express the solution(s) rounded to one decimal place. - cos⁡2x+cos⁡x−1=0\cos ^ { 2 } x + \cos x - 1 = 0cos2x+cosx−1=0

Find the domain of the function f and of its inverse function f−1\mathrm { f } ^ { - 1 }f−1 . - f(x)=−8cos⁡(10x+4)f ( x ) = - 8 \cos ( 10 x + 4 )f(x)=−8cos(10x+4)

Establish the identity. - 1−2sec⁡x−3sec⁡2x−tan⁡2x=1−3sec⁡x1−sec⁡x\frac { 1 - 2 \sec x - 3 \sec ^ { 2 } x } { - \tan ^ { 2 } x } = \frac { 1 - 3 \sec x } { 1 - \sec x }−tan2x1−2secx−3sec2x​=1−secx1−3secx​

Find the exact value of the expression. - sin⁡−122\sin ^ { - 1 } \frac { \sqrt { 2 } } { 2 }sin−122​​

Complete the identity. - sin⁡θcos⁡θ+cos⁡θsin⁡θ= ? \frac { \sin \theta } { \cos \theta } + \frac { \cos \theta } { \sin \theta } = \text { ? }cosθsinθ​+sinθcosθ​= ?

Solve the problem. -The two equal sides of an isosceles triangle measure three feet. Let the angle between the sides measure θ\thetaθ . Find the area A of the triangle as a function of θ2\frac { \theta } { 2 }2θ​ . The answer may include more than one trigonometric function.

Complete the identity. - sin⁡θ2cos⁡θ2=?\sin \frac { \theta } { 2 } \cos \frac { \theta } { 2 } = ?sin2θ​cos2θ​=?

Solve the problem. -Find tan⁡θ2\tan \frac { \theta } { 2 }tan2θ​ , given that tan⁡θ=3\tan \theta = 3tanθ=3 and θ\thetaθ terminates in π<θ<3π/2\pi < \theta < 3 \pi / 2π<θ<3π/2

Find the exact value of the expression. Do not use a calculator. - sin⁡[sin⁡−1(−0.7)]\sin \left[ \sin ^ { - 1 } ( - 0.7 ) \right]sin[sin−1(−0.7)]