Question 1

Express the product as a sum containing only sines or cosines.
-$\sin ( 3 \theta ) \cos ( 4 \theta )$

Accepted Answer

A)  $\sin \cos \left( 12 \theta ^ { 2 } \right)$ 
B)  $\frac { 1 } { 2 } [ \cos ( 7 \theta ) + \sin \theta ]$ 
C)  $\frac { 1 } { 2 } [ \cos ( 7 \theta ) - \cos \theta ]$ 
D)  $\frac { 1 } { 2 } [ \sin ( 7 \theta ) - \sin \theta ]$ 
A)  $\sin \cos \left( 12 \theta ^ { 2 } \right)$ 
B)  $\frac { 1 } { 2 } [ \cos ( 7 \theta ) + \sin \theta ]$ 
C)  $\frac { 1 } { 2 } [ \cos ( 7 \theta ) - \cos \theta ]$ 
D)  $\frac { 1 } { 2 } [ \sin ( 7 \theta ) - \sin \theta ]$

Question 2

Solve the problem.
-$$\tan ^ { 2 } u ( 1 + \cos 2 u ) = 1 - \cos 2 u$$

Accepted Answer

The answer of Solve the problem.
-\[\tan ^ { 2 }...

Question 3

Complete the identity.
-$$\tan ( \pi - \theta ) = \text { ? }$$

Accepted Answer

A)  $- \cot \theta$ 
B)  $- \tan \theta$ 
C)  $\cot \theta$ 
D)  $\tan \theta$ 
A)  $- \cot \theta$ 
B)  $- \tan \theta$ 
C)  $\cot \theta$ 
D)  $\tan \theta$

Question 4

Solve the problem using Snell's Law: $\frac { \sin \theta _ { 1 } } { \sin \theta _ { 2 } } = \frac { v _ { 1 } } { v _ { 2 } }$
-A ray of light near the horizon with an angle of incidence of 77° enters a pool of water and strikes a fish's eye. If the index of refraction is 1.33, what is the angle of refraction (to two decimal places)?

Accepted Answer

A)  42.89° 
B)  46.20° 
C)  47.11° 
D)  43.80° 
A)  42.89° 
B)  46.20° 
C)  47.11° 
D)  43.80°

Question 5

Find the exact value under the given conditions.
-$\sin \alpha = - \frac { 24 } { 25 } , \pi < \alpha < \frac { 3 \pi } { 2 } ; \quad \tan \beta = - \frac { 2 \sqrt { 21 } } { 21 } , \frac { \pi } { 2 } < \beta < \pi \quad$ Find $\cos ( \alpha + \beta )$

Accepted Answer

A)  $\frac { 48 - 7 \sqrt { 21 } } { 125 }$ 
B)  $\frac { 48 + 7 \sqrt { 21 } } { 125 }$ 
C)  $\frac { 14 - 24 \sqrt { 21 } } { 125 }$ 
D)  $\frac { - 14 - 24 \sqrt { 21 } } { 125 }$ 
A)  $\frac { 48 - 7 \sqrt { 21 } } { 125 }$ 
B)  $\frac { 48 + 7 \sqrt { 21 } } { 125 }$ 
C)  $\frac { 14 - 24 \sqrt { 21 } } { 125 }$ 
D)  $\frac { - 14 - 24 \sqrt { 21 } } { 125 }$

Question 6

Solve the problem.
-The average daily temperature T of a city in the United States is approximated by $$T = 55 - 23 \cos \frac { 2 \pi } { 365 } ( t - 30 )$$ where t is in days, $1 \leq t \leq 365$ nd t = 1 corresponds to January 1. For what range of values of t is the average daily
temperature above 70°F? Use a calculator and round answers to the nearest whole number.

Accepted Answer

The answer of Solve the problem.
-The average daily temperature T...

Question 7

Use a calculator to solve the equation on the interval 0 $0 \leq x < 2 \pi$ . Round the answer to one decimal place if necessary.
-$2 x - 3 \cos x = 0$

Accepted Answer

The answer of Use a calculator to solve the equation...

Question 8

Solve the problem.
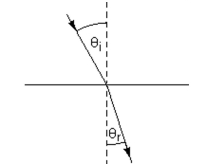
-When light travels from one medium to another-from air to water, for instance-it changes direction. (This is why a pencil, partially submerged in water, looks as though it is bent.) The angle of incidence $\theta _ { \mathrm { r } }$ is the angle in the first medium; the angle of refraction $\theta _ { \mathrm { r } }$ is the second medium. (See illustration.) Each medium has an index of refraction $- \mathrm { n } _ { \mathrm { i } }$ and $\mathrm { n } _ { \mathrm { r } }$, respectively -which can be found in tables. Snell's law relates these quantities in the forr
$$\mathrm { n } _ { \mathrm { i } } \sin \theta _ { \mathrm { i } } = \mathrm { n } _ { \mathrm { r } } \sin \theta _ { \mathrm { r } }$$
Solving for $\theta _ { \mathbf { r } }$, we obtain
$$\theta _ { \mathrm { r } } = \sin ^ { - 1 } \left( \frac { \mathrm { n } _ { \mathrm { i } } } { \mathrm { n } _ { \mathrm { r } } } \sin \theta _ { \mathrm { i } } \right)$$
Find $\theta _ { \mathrm { r } }$ for air $\left( \mathrm { n } _ { \mathrm { i } } = 1.0003 \right)$, methylene iodide $\left( \mathrm { n } _ { \mathrm { r } } = 1.74 \right)$, and $\theta _ { \mathrm { i } } = 14.7 ^ { \circ }$.

Accepted Answer

The answer of Solve the problem.
-When light travels from one...

Question 9

Establish the identity.
-$$\frac { \cos x } { \sec x - 1 } - \frac { \cos x } { \sec x + 1 } = \frac { 2 \cos x } { \tan ^ { 2 } x }$$

Accepted Answer

\[\begin{array} { l } 
\frac { \cos x }

Question 10

Solve the equation on the interval $$0 \leq \theta < 2 \pi$$
-$\sin ( 2 \theta ) + \sin \theta = 0$

Accepted Answer

A)  $\frac { \pi } { 8 } , \frac { 9 \pi } { 8 }$ 
B)  $\frac { \pi } { 4 } , \frac { 3 \pi } { 4 } , \frac { 5 \pi } { 4 } , \frac { 7 \pi } { 4 }$ 
C)  $0 , \frac { 2 \pi } { 3 } , \pi , \frac { 4 \pi } { 3 }$ 
D)  No solution 
A)  $\frac { \pi } { 8 } , \frac { 9 \pi } { 8 }$ 
B)  $\frac { \pi } { 4 } , \frac { 3 \pi } { 4 } , \frac { 5 \pi } { 4 } , \frac { 7 \pi } { 4 }$ 
C)  $0 , \frac { 2 \pi } { 3 } , \pi , \frac { 4 \pi } { 3 }$ 
D)  No solution

Question 11

Find the inverse function $\mathrm { f } ^ { - 1 }$ of the function f.
-$$f ( x ) = 7 \cos x + 4$$

Accepted Answer

A)  $f ^ { - 1 } ( x ) = 7 \cos ^ { - 1 } x + 4$ 
B)  $f ^ { - 1 } ( x ) = \cos ^ { - 1 } \left( \frac { x + 4 } { 7 } \right)$ 
C)  $f ^ { - 1 } ( x ) = \sin \left( \frac { x - 4 } { 7 } \right)$ 
D)  $f ^ { - 1 } ( x ) = \cos ^ { - 1 } \left( \frac { x - 4 } { 7 } \right)$ 
A)  $f ^ { - 1 } ( x ) = 7 \cos ^ { - 1 } x + 4$ 
B)  $f ^ { - 1 } ( x ) = \cos ^ { - 1 } \left( \frac { x + 4 } { 7 } \right)$ 
C)  $f ^ { - 1 } ( x ) = \sin \left( \frac { x - 4 } { 7 } \right)$ 
D)  $f ^ { - 1 } ( x ) = \cos ^ { - 1 } \left( \frac { x - 4 } { 7 } \right)$

Question 12

Use the Half-angle Formulas to find the exact value of the trigonometric function.
-$\sin 165 ^ { \circ }$

Accepted Answer

A)  $- \frac { 1 } { 2 } \sqrt { 2 + \sqrt { 3 } }$ 
B)  $- \frac { 1 } { 2 } \sqrt { 2 - \sqrt { 3 } }$ 
C)  $\frac { 1 } { 2 } \sqrt { 2 - \sqrt { 3 } }$ 
D)  $\frac { 1 } { 2 } \sqrt { 2 + \sqrt { 3 } }$ 
A)  $- \frac { 1 } { 2 } \sqrt { 2 + \sqrt { 3 } }$ 
B)  $- \frac { 1 } { 2 } \sqrt { 2 - \sqrt { 3 } }$ 
C)  $\frac { 1 } { 2 } \sqrt { 2 - \sqrt { 3 } }$ 
D)  $\frac { 1 } { 2 } \sqrt { 2 + \sqrt { 3 } }$

Question 13

Solve the problem.
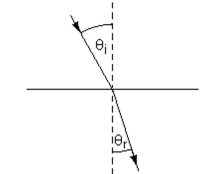
-When light travels from one medium to another-from air to water, for instance-it changes direction. (This is why a pencil, partially submerged in water, looks as though it is bent.) The angle of incidence $\theta _ { \mathrm { i } }$ is the angle in the first medium; the angle of refraction $\theta _ { r }$ is the second medium. (See illustration.) Each medium has an index of refraction $- n _ { i }$ and $n _ { r }$, respectively $-$ which can be found in tables. Snell's law relates these quantities in the forr
$$\mathrm { n } _ { \mathrm { i } } \sin \theta _ { \mathrm { i } } = \mathrm { n } _ { \mathrm { r } } \sin \theta _ { \mathrm { r } }$$
Solving for $\theta _ { \mathbf { r } }$, we obtain
$$\theta _ { \mathrm { r } } = \sin ^ { - 1 } \left( \frac { \mathrm { n } _ { \mathrm { i } } } { \mathrm { n } _ { \mathrm { r } } } \sin \theta _ { \mathrm { i } } \right)$$
Find $\theta _ { \mathrm { r } }$ for fused quartz $\left( \mathrm { n } _ { \mathrm { i } } = 1.46 \right)$, ethyl alcohol $\left( \mathrm { n } _ { \mathrm { r } } = 1.36 \right)$, and $\theta _ { \mathrm { i } } = 8.5 ^ { \circ }$.
 
 a

Accepted Answer

The answer of Solve the problem.
-When light travels from one...

Question 14

Use a graphing utility to solve the equation on the interval 0 $0 ^ { \circ } \leq x < 360 ^ { \circ }$ . Express the solution(s) rounded to one decimal
place.
-$\sin ^ { 2 } x - 8 \sin x + 16 = 0$

Accepted Answer

A)  28.2°, 151.8° 
B)  208.2°, 331.8° 
C)  28.2°, 151.8°, 208.2°, 331.8° 
D)  No solution 
A)  28.2°, 151.8° 
B)  208.2°, 331.8° 
C)  28.2°, 151.8°, 208.2°, 331.8° 
D)  No solution

Question 15

Find the domain of the function f and of its inverse function $\mathrm { f } ^ { - 1 }$ .
-$$f ( x ) = \tan ( x - 4 ) + 7$$

Accepted Answer

A)  Domain of f: $( \infty , \infty )$
Domain of $\mathrm { f } ^ { - 1 } : [ - 8 , - 6 ]$ 
B)  Domain of $f : x \neq \frac { ( 2 k + 1 ) \pi } { 2 } + 7 ; k$ an integer
Domain of $\mathrm { f } ^ { - 1 } : ( \infty , \infty )$ 
C)  Domain of $f : x \neq \frac { ( 2 k + 1 ) \pi } { 2 } ; k$ an integer
Domain of $\mathrm { f } ^ { - 1 } : ( \infty , \infty )$ 
D)  Domain of $\mathrm { f } : [ - 4,4 ]$

Domain of $\mathrm { f } ^ { - 1 } : ( \infty , \infty )$ 
A)  Domain of f: $( \infty , \infty )$
Domain of $\mathrm { f } ^ { - 1 } : [ - 8 , - 6 ]$ 
B)  Domain of $f : x \neq \frac { ( 2 k + 1 ) \pi } { 2 } + 7 ; k$ an integer
Domain of $\mathrm { f } ^ { - 1 } : ( \infty , \infty )$ 
C)  Domain of $f : x \neq \frac { ( 2 k + 1 ) \pi } { 2 } ; k$ an integer
Domain of $\mathrm { f } ^ { - 1 } : ( \infty , \infty )$ 
D)  Domain of $\mathrm { f } : [ - 4,4 ]$

Domain of $\mathrm { f } ^ { - 1 } : ( \infty , \infty )$

Question 16

Find the exact value of the expression.
-$\cos 285 ^ { \circ }$

Accepted Answer

A)  $\frac { \sqrt { 2 } ( \sqrt { 3 } - 1 ) } { 4 }$ 
B)  $- \sqrt { 2 } ( \sqrt { 3 } + 1 )$ 
C)  $- \sqrt { 2 } ( \sqrt { 3 } - 1 )$ 
D)  $- \frac { \sqrt { 2 } ( \sqrt { 3 } - 1 ) } { 4 }$ 
A)  $\frac { \sqrt { 2 } ( \sqrt { 3 } - 1 ) } { 4 }$ 
B)  $- \sqrt { 2 } ( \sqrt { 3 } + 1 )$ 
C)  $- \sqrt { 2 } ( \sqrt { 3 } - 1 )$ 
D)  $- \frac { \sqrt { 2 } ( \sqrt { 3 } - 1 ) } { 4 }$

Question 17

Use a calculator to find the value of the expression rounded to two decimal places.
-$\cos ^ { - 1 } ( 0.3 )$

Accepted Answer

A)  0.30 
B)  72.54 
C)  1.27 
D)  17.46 
A)  0.30 
B)  72.54 
C)  1.27 
D)  17.46

Question 18

Find the exact value of the expression.
-$\cos 20 ^ { \circ } \cos 40 ^ { \circ } - \sin 20 ^ { \circ } \sin 40 ^ { \circ }$

Accepted Answer

A)  $\frac { \sqrt { 3 } } { 2 }$ 
B)  $\sqrt { 3 }$ 
C)  $\frac { 1 } { 2 }$ 
D)  $\frac { 1 } { 4 }$ 
A)  $\frac { \sqrt { 3 } } { 2 }$ 
B)  $\sqrt { 3 }$ 
C)  $\frac { 1 } { 2 }$ 
D)  $\frac { 1 } { 4 }$

Question 19

Solve the equation. Give a general formula for all the solutions.
-$\sin \theta = 0$

Accepted Answer

A)  $\theta = \frac { \pi } { 2 } + k \pi$ 
B)  $\theta = \frac { \pi } { 2 } + 2 \mathrm { k } \pi$ 
C)  $\theta = 0 + \mathrm { k } \pi$ 
D)  $\theta = 0 + 2 \mathrm { k } \pi$ 
A)  $\theta = \frac { \pi } { 2 } + k \pi$ 
B)  $\theta = \frac { \pi } { 2 } + 2 \mathrm { k } \pi$ 
C)  $\theta = 0 + \mathrm { k } \pi$ 
D)  $\theta = 0 + 2 \mathrm { k } \pi$

Question 20

Use the Half-angle Formulas to find the exact value of the trigonometric function.
-$\sin 75 ^ { \circ }$

Accepted Answer

A)  $- \frac { 1 } { 2 } \sqrt { 2 - \sqrt { 3 } }$ 
B)  $- \frac { 1 } { 2 } \sqrt { 2 + \sqrt { 3 } }$ 
C)  $\frac { 1 } { 2 } \sqrt { 2 + \sqrt { 3 } }$ 
D)  $\frac { 1 } { 2 } \sqrt { 2 - \sqrt { 3 } }$ 
A)  $- \frac { 1 } { 2 } \sqrt { 2 - \sqrt { 3 } }$ 
B)  $- \frac { 1 } { 2 } \sqrt { 2 + \sqrt { 3 } }$ 
C)  $\frac { 1 } { 2 } \sqrt { 2 + \sqrt { 3 } }$ 
D)  $\frac { 1 } { 2 } \sqrt { 2 - \sqrt { 3 } }$

Express the product as a sum containing only sines or cosines. - $\sin ( 3 \theta ) \cos ( 4 \theta )$

Solve the problem. - $\tan ^ { 2 } u ( 1 + \cos 2 u ) = 1 - \cos 2 u$

Complete the identity. - $\tan ( \pi - \theta ) = \text { ? }$

Find the exact value under the given conditions. - $\sin \alpha = - \frac { 24 } { 25 } , \pi < \alpha < \frac { 3 \pi } { 2 } ; \quad \tan \beta = - \frac { 2 \sqrt { 21 } } { 21 } , \frac { \pi } { 2 } < \beta < \pi \quad$ Find $\cos ( \alpha + \beta )$

Use a calculator to solve the equation on the interval 0 $0 \leq x < 2 \pi$ . Round the answer to one decimal place if necessary. - $2 x - 3 \cos x = 0$

Establish the identity. - $\frac { \cos x } { \sec x - 1 } - \frac { \cos x } { \sec x + 1 } = \frac { 2 \cos x } { \tan ^ { 2 } x }$

Solve the equation on the interval $0 \leq \theta < 2 \pi$ - $\sin ( 2 \theta ) + \sin \theta = 0$

Find the inverse function $\mathrm { f } ^ { - 1 }$ of the function f. - $f ( x ) = 7 \cos x + 4$

Use the Half-angle Formulas to find the exact value of the trigonometric function. - $\sin 165 ^ { \circ }$

Use a graphing utility to solve the equation on the interval 0 $0 ^ { \circ } \leq x < 360 ^ { \circ }$ . Express the solution(s) rounded to one decimal place. - $\sin ^ { 2 } x - 8 \sin x + 16 = 0$

Find the domain of the function f and of its inverse function $\mathrm { f } ^ { - 1 }$ . - $f ( x ) = \tan ( x - 4 ) + 7$

Find the exact value of the expression. - $\cos 285 ^ { \circ }$

Use a calculator to find the value of the expression rounded to two decimal places. - $\cos ^ { - 1 } ( 0.3 )$

Find the exact value of the expression. - $\cos 20 ^ { \circ } \cos 40 ^ { \circ } - \sin 20 ^ { \circ } \sin 40 ^ { \circ }$

Solve the equation. Give a general formula for all the solutions. - $\sin \theta = 0$

Use the Half-angle Formulas to find the exact value of the trigonometric function. - $\sin 75 ^ { \circ }$

Functions and Their Graphs

Linear and Quadratic Functions

Polynomial and Rational Functions

Exponential and Logarithmic Functions

Trigonometric Functions

Applications of Trigonometric Functions

Polar Coordinates; Vectors

Analytic Geometry

Systems of Equations and Inequalities

Sequences; Induction; the Binomial Theorem

Counting and Probability

A Preview of Calculus: the Limit, Derivative, and Integral of a Function

Review

Filters

Exam 6: Analytic Trigonometry

Express the product as a sum containing only sines or cosines. - sin⁡(3θ)cos⁡(4θ)\sin ( 3 \theta ) \cos ( 4 \theta )sin(3θ)cos(4θ)

Solve the problem. - tan⁡2u(1+cos⁡2u)=1−cos⁡2u\tan ^ { 2 } u ( 1 + \cos 2 u ) = 1 - \cos 2 utan2u(1+cos2u)=1−cos2u

Complete the identity. - tan⁡(π−θ)= ? \tan ( \pi - \theta ) = \text { ? }tan(π−θ)= ?

Use a calculator to solve the equation on the interval 0 0≤x<2π0 \leq x < 2 \pi0≤x<2π . Round the answer to one decimal place if necessary. - 2x−3cos⁡x=02 x - 3 \cos x = 02x−3cosx=0

Establish the identity. - cos⁡xsec⁡x−1−cos⁡xsec⁡x+1=2cos⁡xtan⁡2x\frac { \cos x } { \sec x - 1 } - \frac { \cos x } { \sec x + 1 } = \frac { 2 \cos x } { \tan ^ { 2 } x }secx−1cosx​−secx+1cosx​=tan2x2cosx​

Solve the equation on the interval 0≤θ<2π0 \leq \theta < 2 \pi0≤θ<2π - sin⁡(2θ)+sin⁡θ=0\sin ( 2 \theta ) + \sin \theta = 0sin(2θ)+sinθ=0

Find the inverse function f−1\mathrm { f } ^ { - 1 }f−1 of the function f. - f(x)=7cos⁡x+4f ( x ) = 7 \cos x + 4f(x)=7cosx+4

Use the Half-angle Formulas to find the exact value of the trigonometric function. - sin⁡165∘\sin 165 ^ { \circ }sin165∘

Use a graphing utility to solve the equation on the interval 0 0∘≤x<360∘0 ^ { \circ } \leq x < 360 ^ { \circ }0∘≤x<360∘ . Express the solution(s) rounded to one decimal place. - sin⁡2x−8sin⁡x+16=0\sin ^ { 2 } x - 8 \sin x + 16 = 0sin2x−8sinx+16=0

Find the domain of the function f and of its inverse function f−1\mathrm { f } ^ { - 1 }f−1 . - f(x)=tan⁡(x−4)+7f ( x ) = \tan ( x - 4 ) + 7f(x)=tan(x−4)+7

Find the exact value of the expression. - cos⁡285∘\cos 285 ^ { \circ }cos285∘

Use a calculator to find the value of the expression rounded to two decimal places. - cos⁡−1(0.3)\cos ^ { - 1 } ( 0.3 )cos−1(0.3)

Find the exact value of the expression. - cos⁡20∘cos⁡40∘−sin⁡20∘sin⁡40∘\cos 20 ^ { \circ } \cos 40 ^ { \circ } - \sin 20 ^ { \circ } \sin 40 ^ { \circ }cos20∘cos40∘−sin20∘sin40∘

Solve the equation. Give a general formula for all the solutions. - sin⁡θ=0\sin \theta = 0sinθ=0

Use the Half-angle Formulas to find the exact value of the trigonometric function. - sin⁡75∘\sin 75 ^ { \circ }sin75∘