Exam 4: Exponential and Logarithmic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Solve the problem.
-Gillian has $10,000 to invest in a mutual fund. The average annual rate of return for the past five years was
12.25%. Assuming this rate, determine how long it will take for her investment to double.
(Short Answer)
4.9/5  (27)
(27)
Write as the sum and/or difference of logarithms. Express powers as factors.
-
(Multiple Choice)
4.8/5  (31)
(31)
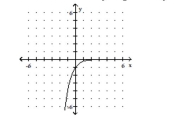
Use transformations to graph the function. Determine the domain, range, and horizontal asymptote of the function.
-
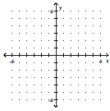 A) domain of ; range of f:
horizontal asymptote:
A) domain of ; range of f:
horizontal asymptote:
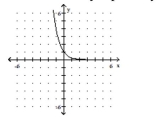 B) domain of ; range of
horizontal asymptote:
B) domain of ; range of
horizontal asymptote:
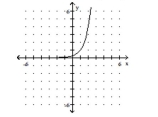 C)
domain of ; range of
horizontal asymptote:
C)
domain of ; range of
horizontal asymptote:
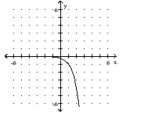 D)
domain of ; range of horizontal asymptote:
D)
domain of ; range of horizontal asymptote:
(Multiple Choice)
4.9/5  (38)
(38)
Decide whether or not the functions are inverses of each other.
-
(Multiple Choice)
5.0/5  (38)
(38)
The Richter scale converts seismographic readings into numbers for measuring the magnitude of an earthquake according to this
function
-Two earthquakes differ by 0.1 when measured on the Richter scale. How would the seismographic readings
differ at a distance of 100 kilometers from the epicenter?
(Essay)
5.0/5  (36)
(36)
Use a graphing calculator to solve the equation. Round your answer to two decimal places.
-
(Multiple Choice)
4.9/5  (36)
(36)
Find the inverse. Determine whether the inverse represents a function.
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Meike earned $1565 in tips while working a summer job at a coffee shop. She wants to use this money to take a
trip to Europe next summer. If she places the money in an account which pays 6.5% compounded continuously,
how much money will she have in nine months?
(Short Answer)
5.0/5  (37)
(37)
Solve the problem.
-A fossilized leaf contains 18% of its normal amount of carbon 14. How old is the fossil (to the nearest year)? Use 5600 years as the half-life of carbon 14.
(Multiple Choice)
4.7/5  (39)
(39)
Change the exponential expression to an equivalent expression involving a logarithm.
-
(Multiple Choice)
4.9/5  (28)
(28)
Use the Change-of-Base Formula and a calculator to evaluate the logarithm. Round your answer to two decimal places.
-
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-Which of the two rates would yield the larger amount in 1 year: compounded monthly or compounded annually?
(Multiple Choice)
4.7/5  (35)
(35)
Showing 181 - 200 of 518
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)