Exam 4: Exponential and Logarithmic Functions

Solve the problem. -The long jump record, in feet, at a particular school can be modeled by $f ( x ) = 19 + 2.5 \ln ( x + 1 )$ where x is the number of years since records began to be kept at the school. What is the record for the long jump 25 years after Record started being kept? Round your answer to the nearest tenth.

Solve the problem. - $\mathrm { pH } = - \log _ { 10 } \left[ \mathrm { H } ^ { + } \right]$ Find the $\left[ \mathrm { H } ^ { + } \right]$ if the $\mathrm { pH } = 1.4$ .

Use a graphing calculator to solve the equation. Round your answer to two decimal places. - $e ^ { x } = - x$

Find the exact value of the logarithmic expression. - $\log _ { 4 } \frac { 1 } { 64 }$

Graph the function. - $f ( x ) = e ^ { 2 x }$ A) B) C) D)

Solve the problem. -In a town whose population is 3000, a disease creates an epidemic. The number of people, N, infected t days after the disease has begun is given by the function $\mathrm { N } ( \mathrm { t } ) = \frac { 3000 } { 1 + 21.2 \mathrm { e } ^ { - 0.54 t } }$ Find the number of infected people after 10 days.

Decide whether the composite functions, f $f \circ g$ nd $\mathbf { g } \circ \mathrm { f }$ f, are equal to x. - $f ( x ) = \frac { 1 } { x } , g ( x ) = x$

Graph the function. - $y = \log _ { 2 } x$ A) B) C) D)

Solve the problem. -The half-life of a radioactive element is 130 days, but your sample will not be useful to you after 80% of the radioactive nuclei originally present have disintegrated. About how many days can you use the sample?

Find the domain of the function. - $f ( x ) = \log _ { 6 } \left( 36 - x ^ { 2 } \right)$

Write the word or phrase that best completes each statement or answers the question. Solve the problem. -To remodel a bathroom, a contractor charges $\$ 25$ per hour plus material costs, which amount to $\$ 3,775$ . Therefore, the total cost to remodel the bathroom is given by $f ( x ) = 25 x + 3,775$ where $x$ is the number of hou the contractor works. Find a formula for $f ^ { - 1 } ( x )$ . What does $f ^ { - 1 } ( x )$ compute?

Write the word or phrase that best completes each statement or answers the question. Solve the problem. -The function $f ( x ) = | x | - 5$ is not one-to-one. (a) Find a suitable restriction on the domain of $\mathrm { f }$ so that the new function that results is one-to-one. (b) Find the inverse of $f$ .

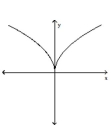
Use the horizontal line test to determine whether the function is one-to-one. -

Find a formula for the inverse of the function described below. -A size 44 dress in Country C is size 2 in Country D. A function that converts dress sizes in Country C to those in Country D is $f ( x ) = \frac { x } { 2 } - 20$ A) $f ^ { - 1 } ( x ) = x + 20$ B) $f ^ { - 1 } ( x ) = 2 x + 20$ C) $f ^ { - 1 } ( x ) = 2 ( x + 20 )$ D) $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = 2 ( \mathrm { x } - 20 )$

Solve the equation. - $3 ( 3 x - 6 ) = 27$

Write as the sum and/or difference of logarithms. Express powers as factors. - $\log _ { 8 } \frac { 11 \sqrt { r } } { s }$

Choose the one alternative that best completes the statement or answers the question. Solve the exponential equation. Use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. - $4 ( x - 1 ) = 19$

Find the value of the expression. -Let $\log _ { b } A = 4$ and $\log _ { b } B = - 5$ . Find $\log _ { b } 2 \sqrt { A B }$ .

The function f is one-to-one. Find its inverse. - $f ( x ) = \frac { 2 } { x - 4 }$

Choose the one alternative that best completes the statement or answers the question. Solve the exponential equation. Use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. - $\mathrm { e } ^ { 2 x } = 4$