Exam 4: Exponential and Logarithmic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Solve the problem.
-Cindy will require $12,000 in 5 years to return to college to get an MBA degree. How much money should she ask her parents for now so that, if she invests it at 11% compounded continuously, she will have enough for
School? (Round your answer to the nearest dollar.)
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-How much money needs to be invested now to get $2000 after 4 years at 8% compounded quarterly? Express your answer to the nearest dollar.
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-An oil well off the Gulf Coast is leaking, with the leak spreading oil over the surface of the gulf as a circle. At any time t, in minutes, after the beginning of the leak, the radius of the oil slick on the surface is r(t) = 3t ft. Find
The area A of the oil slick as a function of time. A)
B)
C)
D)
(Multiple Choice)
4.8/5  (34)
(34)
Change the logarithmic expression to an equivalent expression involving an exponent.
-
(Multiple Choice)
4.8/5  (36)
(36)
Change the logarithmic expression to an equivalent expression involving an exponent.
-
(Multiple Choice)
4.7/5  (28)
(28)
Find the present value. Round to the nearest cent.
-To get $5600 after 8 years at 5% compounded annually
(Multiple Choice)
4.8/5  (30)
(30)
Determine i) the domain of the function, ii) the range of the function, iii) the domain of the inverse, and iv) the range of
the inverse.
-
(Multiple Choice)
4.9/5  (28)
(28)
Solve the problem.
-A venture capital firm invested $2,000,000 in a new company in 1995. In 1999, they sold their stake in the
company for $10,500,000. What was the average annual rate of return on their investment?
(Short Answer)
4.8/5  (36)
(36)
Solve the given exponential equation. Round answer to three decimal places.
-
(Multiple Choice)
4.9/5  (38)
(38)
Find the amount that results from the investment.
-$1,000 invested at 6% compounded annually after a period of 8 years
(Multiple Choice)
4.9/5  (40)
(40)
Use the Change-of-Base Formula and a calculator to evaluate the logarithm. Round your answer to three decimal places.
-
(Multiple Choice)
4.8/5  (31)
(31)
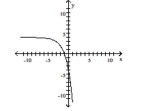
Use transformations to graph the function. Determine the domain, range, and horizontal asymptote of the function.
-
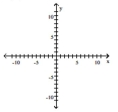 A) domain of ; range of ;
horizontal asymptote:
A) domain of ; range of ;
horizontal asymptote:
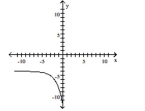 B) domain of ; range of ;
horizontal asymptote:
B) domain of ; range of ;
horizontal asymptote:
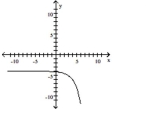 C) domain of ; range of ;
horizontal asymptote:
C) domain of ; range of ;
horizontal asymptote:
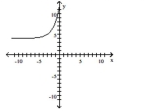 D) domain of ; range of ;
horizontal asymptote:
D) domain of ; range of ;
horizontal asymptote:
(Multiple Choice)
4.8/5  (32)
(32)
The Richter scale converts seismographic readings into numbers for measuring the magnitude of an earthquake according to this
function
-What is the magnitude of an earthquake whose seismographic reading is 6.6 millimeters at a distance of 100 kilometers from its epicenter? Round the answer to the nearest tenth.
(Multiple Choice)
4.9/5  (30)
(30)
Showing 61 - 80 of 518
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)