Exam 4: Exponential and Logarithmic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Solve the problem.
-A city is growing at the rate of 0.5% annually. If there were 3,110,000 residents in the city in 1,995, find how many (to the nearest ten-thousand) were living in that city in 2000. Use
(Multiple Choice)
4.8/5  (30)
(30)
Use a calculator to find the natural logarithm correct to four decimal places.
-
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-A thermometer reading 84°F is placed inside a cold storage room with a constant temperature of 38°F. If the thermometer reads 77°F in 11 minutes, how long before it reaches 56°F? Assume the cooling follows Newton's Law
Of Cooling: (Round your answer to the nearest whole minute.)
(Multiple Choice)
4.9/5  (39)
(39)
For the given functions f and g, find the requested composite function.
- Find
(Multiple Choice)
4.9/5  (28)
(28)
Solve the given exponential equation. Round answer to three decimal places.
-
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-During 1991, 200,000 people visited Rave Amusement Park. During 1997, the number had grown to 834,000. If the number of visitors to the park obeys the law of uninhibited growth, find the exponential growth function
That models this data. A)
B)
C)
D)
(Multiple Choice)
4.9/5  (30)
(30)
The graph of a one-to-one function f is given. Draw the graph of the inverse function f-1 as a dashed line or curve.
-
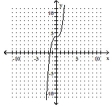 A)
A)
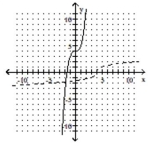 B)
B)
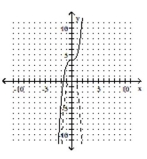
(Multiple Choice)
4.8/5  (33)
(33)
Decide whether the composite functions, f nd f, are equal to x.
-
(Multiple Choice)
4.9/5  (28)
(28)
The loudness of a sound of intensity x, measured in watts per square meter, is defined as L(
-At a recent Phish rock concert, sound intensity reached a level of 0.50 watt per square meter. To the nearest
whole number, calculate the loudness of this sound in decibels.
(Short Answer)
4.8/5  (31)
(31)
Write as the sum and/or difference of logarithms. Express powers as factors.
-
(Essay)
4.8/5  (43)
(43)
Solve the problem.
-How long does it take $1700 to double if it is invested at 5% interest, compounded monthly? Round your
answer to the nearest tenth.
(Short Answer)
4.9/5  (35)
(35)
Solve the problem.
-The value of a particular investment follows a pattern of exponential growth. In the year 2000, you invested money in a money market account. The value of your investment t years after 2000 is given by the exponential
Growth model A . By what percentage is the account increasing each year?
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-The rates of death (in number of deaths per 100,000 population) for 20-24 year olds in the United States
between 1985-1993 are given below. (Source: NCHS Data Warehouse) Year Rate of Death 1985 134.9 1987 154.7 1989 162.9 1991 174.5 1993 182.2 A logarithmic equation that models this data i 56 ln x where x represents the number of years since
1980 and y represents the rate of death in that year. Use this equation to predict the year in which the rate of
death for 20-24 year olds first exceeds 200.
(Short Answer)
4.8/5  (39)
(39)
Graph the function using a graphing utility and the Change-of-Base Formula.
- y=x
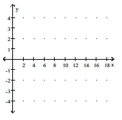 A)
A)
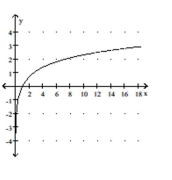 B)
B)
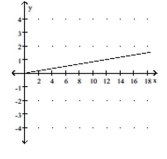 C)
C)
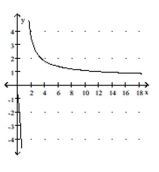 D)
D)
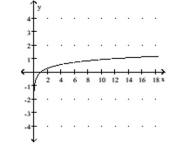
(Multiple Choice)
4.9/5  (33)
(33)
Showing 141 - 160 of 518
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)