Question 1

Find the domain of the function.
-$$f ( x ) = \log _ { 10 } \left( \frac { x + 8 } { x - 8 } \right)$$

Accepted Answer

A)  $( 8 , \infty )$ 
B)  $( - \infty , - 8 ) \cup ( 8 , \infty )$ 
C)  $( - \infty , - 8 )$ 
D)  $( - 8,8 )$ 
A)  $( 8 , \infty )$ 
B)  $( - \infty , - 8 ) \cup ( 8 , \infty )$ 
C)  $( - \infty , - 8 )$ 
D)  $( - 8,8 )$

Question 2

The Richter scale converts seismographic readings into numbers for measuring the magnitude of an earthquake according to this
function $$M ( x ) = \log \left( \frac { x } { x _ { 0 } } \right) , \text { where } x _ { 0 } = 10 ^ { - 3 }$$
-What is the magnitude of an earthquake whose seismographic reading is 0.94 millimeters at a distance of 100
kilometers from its epicenter?

Accepted Answer

The answer of The Richter scale converts seismographic readings into...

Question 3

Change the logarithmic expression to an equivalent expression involving an exponent.
-$$\log _ { 2 } 8 = 3$$

Accepted Answer

A)  $2 ^ { 8 } = 3$ 
B)  $2 ^ { 3 } = 8$ 
C)  $8 ^ { 3 } = 2$ 
D)  $3 ^ { 2 } = 8$ 
A)  $2 ^ { 8 } = 3$ 
B)  $2 ^ { 3 } = 8$ 
C)  $8 ^ { 3 } = 2$ 
D)  $3 ^ { 2 } = 8$

Question 4

Find a formula for the inverse of the function described below.
-$32 ^ { \circ }$ Fahrenheit $= 0 ^ { \circ }$ Celsius. A function that converts temperatures in Celsius to those in Fahrenheit is $f ( x ) = \frac { 9 } { 5 } x + 32$

Accepted Answer

A)  $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { 9 } { 5 } \mathrm { x } + 32$ 
B)  $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { 5 } { 9 } ( \mathrm { x } - 32 )$ 
C)  $f ^ { - 1 } ( x ) = \frac { 5 } { 9 } ( x + 32 )$ 
D)  $f ^ { - 1 } ( x ) = x + 32$ 
A)  $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { 9 } { 5 } \mathrm { x } + 32$ 
B)  $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { 5 } { 9 } ( \mathrm { x } - 32 )$ 
C)  $f ^ { - 1 } ( x ) = \frac { 5 } { 9 } ( x + 32 )$ 
D)  $f ^ { - 1 } ( x ) = x + 32$

Question 5

Find a formula for the inverse of the function described below.
-A size 4 dress in Country C is size 40 in Country D. A function that converts dress sizes in Country C to those in Country D is f(x) = 2(x + 16). A) $f ^ { - 1 } ( x ) = \frac { x } { 2 } + 16$

Accepted Answer

B)  $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \mathrm { x } - 16$ 
C)  $f ^ { - 1 } ( x ) = \frac { x } { 2 } - 16$ 
D)  $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { \mathrm { x } - 16 } { 2 }$ 
B)  $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \mathrm { x } - 16$ 
C)  $f ^ { - 1 } ( x ) = \frac { x } { 2 } - 16$ 
D)  $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = \frac { \mathrm { x } - 16 } { 2 }$

Question 6

For the given functions f and g, find the requested composite function.
-$$f ( x ) = \frac { x - 10 } { 2 } , \quad g ( x ) = 2 x + 10 ; \quad \text { Find } ( g \circ f ) ( x )$$

Accepted Answer

A)  x 
B)  2x + 10 
C)  x - 5 
D)  x + 20 
A)  x 
B)  2x + 10 
C)  x - 5 
D)  x + 20

Question 7

Use the properties of logarithms to find the exact value of the expression. Do not use a calculator.
-$\log _ { 4 } 21 \cdot \log _ { 21 } 64$

Accepted Answer

A)  21 
B)  4 
C)  64 
D)  3 
A)  21 
B)  4 
C)  64 
D)  3

Question 8

Solve the problem.
-The rates of death (in number of deaths per 100,000 population) for 1-4 year olds in the United States between
1980-1995 are given below. (Source: NCHS Data Warehouse) $$\begin{array} { c | c } 
\text { Year } & \text { Rate of Death } \
\hline 1980 & 91.4 \
\hline 1985 & 74.5 \
\hline 1990 & 69.3 \
\hline 1995 & 61.3
\end{array}$$ A logarithmic equation that models this data i $$y = 822.99 - 167.55 \ln x$$ 167.55 ln x where x represents the number of years
since 1900. Use this equation to predict the rate of death for 1-4 year olds in 2005.

Accepted Answer

43.2 death

Question 9

Solve the equation.
-$\log ( 5 + x ) - \log ( x - 4 ) = \log 2$

Accepted Answer

A)  $\left\{ \frac { 1 } { 2 } \right\}$ 
B)  $\varnothing$ 
C)  $\{ 13 \}$ 
D)  $\{ - 13 \}$ 
A)  $\left\{ \frac { 1 } { 2 } \right\}$ 
B)  $\varnothing$ 
C)  $\{ 13 \}$ 
D)  $\{ - 13 \}$

Question 10

The graph of an exponential function is given. Match the graph to one of the following functions.
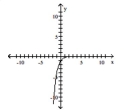-  A) $f ( x ) = - 4 ^ { x }$

Accepted Answer

B)  $f ( x ) = 4 ^ { - x }$ 
C)  $f ( x ) = - 4 ^ { - x }$ 
D)  $f ( x ) = 4 ^ { x }$ 
B)  $f ( x ) = 4 ^ { - x }$ 
C)  $f ( x ) = - 4 ^ { - x }$ 
D)  $f ( x ) = 4 ^ { x }$

Question 11

The loudness of a sound of intensity x, measured in watts per square meter, is defined as L( $$L ( x ) = \log \left( \frac { x } { x _ { 0 } } \right) , \text { where } x _ { 0 } = 10 ^ { - 3 }$$
-At a rock concert by The Who, the music registered a loudness level of 120 decibels. The human threshold of
pain due to sound averages 130 decibels. Compute the ratio of the intensities associated with these two loudness
level to determine by how much the intensity of a sound that crosses the human threshold of pain exceeds that
of this particular rock concert.

Accepted Answer

The intensity of a sound that

Question 12

The function f is one-to-one. Find its inverse.
-$$f ( x ) = 2 x$$

Accepted Answer

A)  $f ^ { - 1 } ( x ) = - 2 x$ 
B)  $f ^ { - 1 } ( x ) = \frac { x } { 2 }$ 
C)  $f ^ { - 1 } ( x ) = \frac { 2 } { x }$ 
D)  $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = 2 \mathrm { x }$ 
A)  $f ^ { - 1 } ( x ) = - 2 x$ 
B)  $f ^ { - 1 } ( x ) = \frac { x } { 2 }$ 
C)  $f ^ { - 1 } ( x ) = \frac { 2 } { x }$ 
D)  $\mathrm { f } ^ { - 1 } ( \mathrm { x } ) = 2 \mathrm { x }$

Question 13

Indicate whether the function is one-to-one.
-{(12, -18), (-12, -18), (20, -8)}

Accepted Answer

A)  Yes 
B)  No 
A)  Yes 
B)  No

Question 14

Solve the problem.
-The logistic growth functi $f ( t ) = \frac { 24,000 } { 1 + 599.0 \mathrm { e } ^ { - 1.8 t } }$ models the number of people who have become ill with a particular infection t weeks after its initial outbreak in a particular community. What is the limiting size of the
Population that becomes ill?

Accepted Answer

A)  599 people 
B)  24,000 people 
C)  600 people 
D)  48,000 people 
A)  599 people 
B)  24,000 people 
C)  600 people 
D)  48,000 people

Question 15

Approximate the value using a calculator. Express answer rounded to three decimal places.
-$5.52 ^ { 2.828 }$

Accepted Answer

A)  310.575 
B)  12,459.589 
C)  15.611 
D)  125.373 
A)  310.575 
B)  12,459.589 
C)  15.611 
D)  125.373

Question 16

Solve the equation.
-$( 8 ) x + 1 = \left( \frac { 2 } { 4 } \right) ^ { x - 1 }$

Accepted Answer

A)  $\left\{ - \frac { 1 } { 2 } \right\}$ 
B)  $\{ - 1 \}$ 
C)  $\left\{ \frac { 1 } { 2 } \right\}$ 
D)  $\left\{ - \frac { 1 } { 4 } \right\}$ 
A)  $\left\{ - \frac { 1 } { 2 } \right\}$ 
B)  $\{ - 1 \}$ 
C)  $\left\{ \frac { 1 } { 2 } \right\}$ 
D)  $\left\{ - \frac { 1 } { 4 } \right\}$

Question 17

Use a graphing calculator to solve the equation. Round your answer to two decimal places.
-$e ^ { x } = x ^ { 2 } - 1$

Accepted Answer

A)  {-0.71} 
B)  {-1.15} 
C)  {0} 
D)  {2.54} 
A)  {-0.71} 
B)  {-1.15} 
C)  {0} 
D)  {2.54}

Question 18

For the given functions f and g, find the requested composite function value.
-$f ( x ) = 5 x + 8 , \quad g ( x ) = - 1 / x ; \quad$ Find $( g \circ f ) ( 3 )$.

Accepted Answer

A)  $- \frac { 1 } { 23 }$ 
B)  $\frac { 19 } { 3 }$ 
C)  $\frac { 68 } { 3 }$ 
D)  $- \frac { 23 } { 3 }$ 
A)  $- \frac { 1 } { 23 }$ 
B)  $\frac { 19 } { 3 }$ 
C)  $\frac { 68 } { 3 }$ 
D)  $- \frac { 23 } { 3 }$

Question 19

Write the word or phrase that best completes each statement or answers the question.
Solve the problem.
-The weight W of a bird's brain (in ounces) is related to the volume V of the bird's skull (in cubic ounces)
through the function W(V) $$W ( V ) = 3.55 \sqrt [ 3 ] { V } + 1.23$$ (a) Express the skull volume V as a function of brain weight W.
(b) Predict the skull volume of a bird whose brain weighs 3 oz.

Accepted Answer

The answer of Write the word or phrase that best...

Question 20

Approximate the value using a calculator. Express answer rounded to three decimal places.
-$2.9 ^ { \pi }$

Accepted Answer

A)  9.111 
B)  36.462 
C)  28.357 
D)  27.652 
A)  9.111 
B)  36.462 
C)  28.357 
D)  27.652

Find the domain of the function. - $f ( x ) = \log _ { 10 } \left( \frac { x + 8 } { x - 8 } \right)$

Change the logarithmic expression to an equivalent expression involving an exponent. - $\log _ { 2 } 8 = 3$

Find a formula for the inverse of the function described below. - $32 ^ { \circ }$ Fahrenheit $= 0 ^ { \circ }$ Celsius. A function that converts temperatures in Celsius to those in Fahrenheit is $f ( x ) = \frac { 9 } { 5 } x + 32$

For the given functions f and g, find the requested composite function. - $f ( x ) = \frac { x - 10 } { 2 } , \quad g ( x ) = 2 x + 10 ; \quad \text { Find } ( g \circ f ) ( x )$

Use the properties of logarithms to find the exact value of the expression. Do not use a calculator. - $\log _ { 4 } 21 \cdot \log _ { 21 } 64$

Solve the equation. - $\log ( 5 + x ) - \log ( x - 4 ) = \log 2$

The function f is one-to-one. Find its inverse. - $f ( x ) = 2 x$

Indicate whether the function is one-to-one. -{(12, -18), (-12, -18), (20, -8)}

Approximate the value using a calculator. Express answer rounded to three decimal places. - $5.52 ^ { 2.828 }$

Solve the equation. - $( 8 ) x + 1 = \left( \frac { 2 } { 4 } \right) ^ { x - 1 }$

Use a graphing calculator to solve the equation. Round your answer to two decimal places. - $e ^ { x } = x ^ { 2 } - 1$

For the given functions f and g, find the requested composite function value. - $f ( x ) = 5 x + 8 , \quad g ( x ) = - 1 / x ; \quad$ Find $( g \circ f ) ( 3 )$ .

Approximate the value using a calculator. Express answer rounded to three decimal places. - $2.9 ^ { \pi }$

Functions and Their Graphs

Linear and Quadratic Functions

Polynomial and Rational Functions

Trigonometric Functions

Analytic Trigonometry

Applications of Trigonometric Functions

Polar Coordinates; Vectors

Analytic Geometry

Systems of Equations and Inequalities

Sequences; Induction; the Binomial Theorem

Counting and Probability

A Preview of Calculus: the Limit, Derivative, and Integral of a Function

Review

Filters

Exam 4: Exponential and Logarithmic Functions

Find the domain of the function. - f(x)=log⁡10(x+8x−8)f ( x ) = \log _ { 10 } \left( \frac { x + 8 } { x - 8 } \right)f(x)=log10​(x−8x+8​)

Change the logarithmic expression to an equivalent expression involving an exponent. - log⁡28=3\log _ { 2 } 8 = 3log2​8=3

Find a formula for the inverse of the function described below. - 32∘32 ^ { \circ }32∘ Fahrenheit =0∘= 0 ^ { \circ }=0∘ Celsius. A function that converts temperatures in Celsius to those in Fahrenheit is f(x)=95x+32f ( x ) = \frac { 9 } { 5 } x + 32f(x)=59​x+32

For the given functions f and g, find the requested composite function. - f(x)=x−102,g(x)=2x+10; Find (g∘f)(x)f ( x ) = \frac { x - 10 } { 2 } , \quad g ( x ) = 2 x + 10 ; \quad \text { Find } ( g \circ f ) ( x )f(x)=2x−10​,g(x)=2x+10; Find (g∘f)(x)

Use the properties of logarithms to find the exact value of the expression. Do not use a calculator. - log⁡421⋅log⁡2164\log _ { 4 } 21 \cdot \log _ { 21 } 64log4​21⋅log21​64

Solve the equation. - log⁡(5+x)−log⁡(x−4)=log⁡2\log ( 5 + x ) - \log ( x - 4 ) = \log 2log(5+x)−log(x−4)=log2

The graph of an exponential function is given. Match the graph to one of the following functions. - A) f(x)=−4xf ( x ) = - 4 ^ { x }f(x)=−4x B) f(x)=4−xf ( x ) = 4 ^ { - x }f(x)=4−x C) f(x)=−4−xf ( x ) = - 4 ^ { - x }f(x)=−4−x D) f(x)=4xf ( x ) = 4 ^ { x }f(x)=4x

The function f is one-to-one. Find its inverse. - f(x)=2xf ( x ) = 2 xf(x)=2x