Exam 4: Exponential and Logarithmic Functions

The graph of an exponential function is given. Match the graph to one of the following functions. -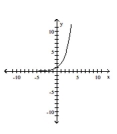 A) $f ( x ) = 2 ^ { x + 2 }$ B) $f ( x ) = 2 ^ { x } - 2$ C) $f ( x ) = 2 ^ { x } + 2$ D) $f ( x ) = 2 ^ { x }$

Solve the problem. -The functio $\mathrm { A } = \mathrm { A } _ { \mathrm { O } } \mathrm { e } ^ { - 0.01386 \mathrm { x } }$ models the amount in pounds of a particular radioactive material stored in a concrete vault, where x is the number of years since the material was put into the vault. If 600 pounds of the Material are placed in the vault, how much time will need to pass for only 99 pounds to remain?

Solve the problem. -After introducing an inhibitor into a culture of luminescent bacteria, a scientist monitors the luminosity produced by the culture. Use a graphing utility to fit a logarithmic function to the data. Predict the luminosity After 20 hours. Time, hrs 2 3 4 5 8 10 15 Luminosity 77.4 60.8 54.5 45.8 30.0 24.3 10.5

The loudness of a sound of intensity x, measured in watts per square meter, is defined as L( $L ( x ) = \log \left( \frac { x } { x _ { 0 } } \right) , \text { where } x _ { 0 } = 10 ^ { - 3 }$ -A particular Boeing 747 jetliner produces noise at a loudness level of 113 decibels. Find the intensity level (round to the nearest hundredth) in watt per square meter for this noise.

Solve the problem. -A fully cooked turkey is taken out of an oven set at 200°C (Celsius) and placed in a sink of chilled water of temperature 4°C. After 3 minutes, the temperature of the turkey is measured to be 50°C. How long (to the nearest minute) will it take for the temperature of the turkey to reach 15°C? Assume the cooling follows Newton's Law of Cooling: $\mathrm { U } = \mathrm { T } + \left( \mathrm { U } _ { \mathrm { O } } - \mathrm { T } \right) \mathrm { e } ^ { \mathrm { kt } }$ (Round your answer to the nearest minute.)

Approximate the value using a calculator. Express answer rounded to three decimal places. - $3.2 ^ { 2.84 }$

Solve the problem. -A rumor is spread at an elementary school with 1200 students according to the model $\mathrm { N } = 1200 \left( 1 - \mathrm { e } ^ { - 0.16 \mathrm {~d} } \right)$ where N is the number of students who have heard the rumor and d is the number of days that have elapsed since the rumor began. How many students will have heard the rumor after 5 days?

The graph of a logarithmic function is shown. Select the function which matches the graph. -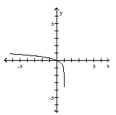 A) $y = \log ( x - 1 )$ B) $y = \log ( x ) - 1$ C) $y = \log ( 1 - x )$ D) $y = 1 - \log ( x )$

Solve the equation. - $\frac { 1 } { 3 } \log _ { 2 } ( x + 6 ) = \log _ { 8 } ( 3 x )$

Solve the problem. -An airline charter service charges a fare per person of $350 plus $20 for each unsold seat. The airplane holds 125 passengers. Let x represent the number of unsold seats and write an expression for the total revenue R for a Charter flight. A) $R ( x ) = ( 125 - x ) ( 350 + 20 x )$ or $43,750 + 2,150 x - 20 x ^ { 2 }$ B) $R ( x ) = 125 ( 350 + 20 x )$ or $43,750 + 2,500 x$ C) $R ( x ) = x ( 350 + 20 x )$ or $350 x + 20 x ^ { 2 }$ D) $R ( x ) = ( 125 - x ) ( 350 + 20 x )$ or $43,750 + 2,500 x - 20 x ^ { 2 }$

Find the exact value of the logarithmic expression. - $\log _ { 5 } \frac { 1 } { 25 }$

Find the domain of the function. - $f ( x ) = \log _ { 10 } \left( x ^ { 2 } - 16 x + 63 \right)$

Evaluate the expression using the values given in the table. - ()(3) 1 7 10 12 () -2 10 0 12 x -5 -2 1 3 g(x) 1 -7 7 10

Solve the problem. -A life insurance company uses the following rate table for annual premiums for women for term life insurance. Use a graphing utility to fit an exponential function to the data. Predict the annual premium for a woman aged 70 years. Age 35 40 45 50 55 60 65 Premium \ 103 \ 133 \ 190 \ 255 \ 360 \ 503 \ 818

Solve the problem. -If a single pane of glass obliterates 15% of the light passing through it, then the percent P of light that passes through n successive panes can be approximated by the equation $P = 100 e ^ { - 0.15 n }$ How many panes are necessary to block at least 50% of the light?

The function f is one-to-one. Find its inverse. - $f ( x ) = \frac { 3 x - 6 } { 8 x - 8 }$

Solve the equation. - $9 ^ { 7 x + 3 } = 27$

Find the domain of the function. - $f ( x ) = \log ( x - 6 )$

Find the present value. Round to the nearest cent. -To get $25,000 after 6 years at 10% compounded semiannually

The function f is one-to-one. Find its inverse. - $f ( x ) = \sqrt { x - 1 }$