Exam 4: Exponential and Logarithmic Functions

Solve the problem. -The logistic growth model $P ( t ) = \frac { 900 } { 1 + 21.5 e ^ { - 0.352 t } }$ represents the population of a bacterium in a culture tube after t hours. When will the amount of bacteria be 760?

Approximate the value using a calculator. Express answer rounded to three decimal places. - $5 ^{\sqrt { 7 }}$

Graph the function. - $f ( x ) = 2 e ^ { x }$ A) B) C) D)

For the given functions f and g, find the requested composite function. - $f ( x ) = \frac { 7 } { x - 3 } , g ( x ) = \frac { 2 } { 5 x } ; \quad \text { Find } ( f \circ g ) ( x )$ A) $\frac { 35 x } { 2 - 15 x }$ B) $\frac { 7 x } { 2 - 15 x }$ C) $\frac { 2 x - 6 } { 35 x }$ D) $\frac { 35 x } { 2 + 15 x }$

Solve the problem. -Larry has $2,000 to invest and needs $2,500 in 13 years. What annual rate of return will he need to get in order to accomplish his goal? (Round your answer to two decimals.)

Write as the sum and/or difference of logarithms. Express powers as factors. - $\log _ { W } \left( \frac { 13 x } { 2 } \right)$

Graph the function. - $f(x)=2-e^{-0.95 x}$ A) B) C) D)

Solve the problem. -Data representing the price and quantity demanded for hand-held electronic organizers were analyzed every day for 15 days. The logarithmic function of best fit to the data was found to be $\mathrm { p } = 398 - 73 \ln ( \mathrm { q } )$ Use this to predict the number of hand-held electronic organizers that would be demanded if the price were $275.

Write as the sum and/or difference of logarithms. Express powers as factors. - $\log _ { 4 } \sqrt { 7 x }$

Change the exponential expression to an equivalent expression involving a logarithm. - $6 ^ { 5 } = 7776$

The graph of a logarithmic function is shown. Select the function which matches the graph. -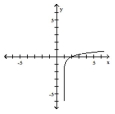 A) $y = \log ( x ) - 1$ B) $y = \log ( 1 - x )$ C) $y = \log ( x - 1 )$ D) $y = 1 - \log ( x )$

Find the amount that results from the investment. -$1,000 invested at 4% compounded semiannually after a period of 6 years

The graph of a logarithmic function is shown. Select the function which matches the graph. -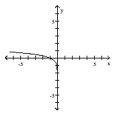 A) $y = \log ( - x )$ B) $y = - \log ( - x )$ C) $y = \log ( x )$ D) $y = - \log ( x )$

Solve the equation. - $4 ^ { x } = 256$

Solve the problem. -A thermometer reading 33°F is brought into a room with a constant temperature of 80°F. If the thermometer reads 45°F after 4 minutes, what will it read after being in the room for 6 minutes? Assume the cooling follows Newton's Law of Cooling: $\mathrm { U } = \mathrm { T } + \left( \mathrm { U } _ { \mathrm { O } } - \mathrm { T } \right) \mathrm { e } ^ { \mathrm { kt } }$ (Round your answer to two decimal places.)

Find the present value. Round to the nearest cent. -To get $6500 after 6 years at 7% compounded quarterly

Solve the problem. -Sandy manages a ceramics shop and uses a 650°F kiln to fire ceramic greenware. After turning off her kiln, she must wait until its temperature gauge reaches 205°F before opening it and removing the ceramic pieces. If room Temperature is 70°F and the gauge reads 500°F in 8 minutes, how long must she wait before opening the kiln? Assume the kiln cools according to Newton's Law of Cooling: $\mathrm { U } = \mathrm { T } + \left( \mathrm { U } _ { \mathrm { O } } - \mathrm { T } \right) \mathrm { e } ^ { \mathrm { kt } }$ (Round your answer to the nearest whole minute.)

Find the domain of the function. - $f ( x ) = \ln \sqrt { x }$