Exam 4: Exponential and Logarithmic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
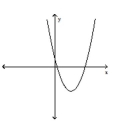
Use the horizontal line test to determine whether the function is one-to-one.
-
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-The population P of a predator mammal depends upon the number x of a smaller animal that is its primary food source. The population s of the smaller animal depends upon the amount a of a certain plant that is its
Primary food source. If and s(a) = 2a + 5, what is the relationship between the predator mammal
And the plant food source? A)
B)
C)
D)
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-The formula D can be used to find the number of milligrams D of a certain drug in a patient's bloodstream h hours after the drug has been given. When the number of milligrams reaches 4, the drug is to be
Given again. What is the time between injections?
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-John Forgetsalot deposited $100 at a 3% annual interest rate in a savings account fifty years ago, and then he
promptly forgot he had done it. Recently, he was cleaning out his home office and discovered the forgotten
bank book. How much money is in the account?
(Short Answer)
4.8/5  (33)
(33)
Use the properties of logarithms to find the exact value of the expression. Do not use a calculator.
-
(Multiple Choice)
4.9/5  (33)
(33)
Choose the one alternative that best completes the statement or answers the question.
Solve the exponential equation. Use a calculator to obtain a decimal approximation, correct to two decimal places, for the
solution.
-
(Multiple Choice)
4.8/5  (36)
(36)
For the given functions f and g, find the requested composite function value.
-
(Multiple Choice)
4.8/5  (37)
(37)
The graph of a one-to-one function f is given. Draw the graph of the inverse function f-1 as a dashed line or curve.
-
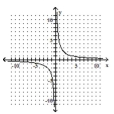 A) Function is its own inverse
A) Function is its own inverse
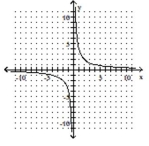 B)
B)
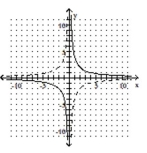
(Multiple Choice)
4.9/5  (39)
(39)
Solve the problem.
-A biologist has a bacteria sample. She records the amount of bacteria every week for 8 weeks and finds that the
exponential function of best fit to the data i . Express the function of best fit in the form
(Essay)
4.9/5  (47)
(47)
Use the Change-of-Base Formula and a calculator to evaluate the logarithm. Round your answer to two decimal places.
-
(Multiple Choice)
4.9/5  (32)
(32)
For the given functions f and g, find the requested composite function value.
- Find
(Multiple Choice)
4.9/5  (35)
(35)
Decide whether the composite functions, f nd f, are equal to x.
-
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-The size P of a small herbivore population at time t (in years) obeys the function if they have enough food and the predator population stays constant. After how many years will the population reach 1,600?
(Multiple Choice)
4.8/5  (33)
(33)
Decide whether or not the functions are inverses of each other.
-
(Multiple Choice)
4.8/5  (37)
(37)
Solve the equation. Express irrational answers in exact form and as a decimal rounded to 3 decimal places.
-
(Multiple Choice)
4.8/5  (30)
(30)
Showing 301 - 320 of 518
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)