Exam 4: Exponential and Logarithmic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
For the given functions f and g, find the requested composite function value.
- Find .
(Multiple Choice)
4.9/5  (40)
(40)
Find the present value. Round to the nearest cent.
-To get $10,000 after 3 years at 6% compounded monthly
(Multiple Choice)
4.8/5  (28)
(28)
Find the effective rate of interest.
- % compounded monthly
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-The logistic growth functi describes the population of a species of butterflies t months after they are introduced to a non-threatening habitat. What is the limiting size of the butterfly population that the
Habitat will sustain?
(Multiple Choice)
4.9/5  (39)
(39)
Write as the sum and/or difference of logarithms. Express powers as factors.
-
(Multiple Choice)
4.8/5  (40)
(40)
Determine whether the given function is exponential or not. If it is exponential, identify the value of the base a.
- () -1 3 0 7 1 11 2 15 3 19
(Multiple Choice)
4.7/5  (35)
(35)
Solve the problem.
-Strontium 90 decays at a constant rate of 2.44% per year. Therefore, the equation for the amount P of strontium 90 after t years is P = P0 e-0.0244t. How long will it take for 15 grams of strontium to decay to 5 grams? Round
Answer to 2 decimal places.
(Multiple Choice)
4.8/5  (29)
(29)
Change the exponential expression to an equivalent expression involving a logarithm.
-
(Multiple Choice)
4.7/5  (37)
(37)
Solve the problem.
-The formul models the population of a particular city, in thousands, t years after 1998. When will the population of the city reach 287 thousand?
(Multiple Choice)
4.9/5  (33)
(33)
The graph of a one-to-one function f is given. Draw the graph of the inverse function f-1 as a dashed line or curve.
-
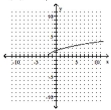 A)
A)
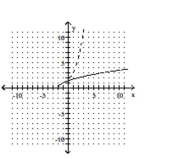 B)
B)
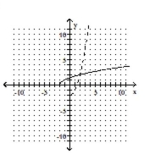
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-Conservationists tagged 130 black-nosed rabbits in a national forest in 1990. In 1,991, they tagged 260 black-nosed rabbits in the same range. If the rabbit population follows the exponential law, how many rabbits
Will be in the range 9 years from 1990?
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-In 1992, the population of a country was estimated at 5 million. For any subsequent year, the population, P(t) (in
millions), can be modeled using the equation , where t is the number of years since
1992. Determine the year when the population will be 39 million.
(Essay)
4.8/5  (39)
(39)
Solve the problem.
-Find a so that the graph of contains the point .
(Multiple Choice)
4.8/5  (35)
(35)
Showing 41 - 60 of 518
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)