Exam 5: Discrete Probability Distributions

The Vardon Exploration Company is getting ready to leave for South America to explore for oil. One piece of equipment requires 10 batteries that must operate for more than 2 hours. The batteries being used have a 15 percent chance of failing within 2 hours. The exploration leader plans to take 15 batteries. Assuming that the conditions of the binomial apply, the probability that the supply of batteries will not contain enough good ones to operate the equipment is:

A corporation has 11 manufacturing plants. Of these, 7 are domestic and 4 are located outside the United States. Each year a performance evaluation is conducted for 4 randomly selected plants. What is the probability that a performance evaluation will include exactly 1 plant outside the United States?

The number of customers who arrive at a fast food business during a one-hour period is known to be Poisson distributed with a mean equal to 8.60. The probability that exactly 8 customers will arrive in a one-hour period is 0.1366.

Madam Helga claims to be psychic. A national TV talk personality plans to test her in a live TV broadcast. The process will entail asking Madam Helga a series of 20 independent questions with yes/no answers. The questions would be of the nature that she could not have any way of knowing the answer from prior knowledge. She will be considered psychic if she correctly answers more than a specified number (called the cut-off) of the questions. The cut-off must be set so that the chance of guessing that number or more is no greater than 5 percent. The cut-off value should be:

The manager of a movie theater has determined that the distribution of customers arriving at the concession stand is Poisson distributed with a standard deviation equal to 2 people per 10 minutes. What is the probability that more than 3 customers arrive during a 10-minute period?

The binomial distribution is frequently used to help companies decide whether to accept or reject a shipment based on the results of a random sample of items from the shipment. For instance, suppose a contract calls for, at most, 10 percent of the items in a shipment to be red. To check this without looking at every item in the large shipment, a sample of n = 10 items is selected. If 1 or fewer are red, the shipment is accepted; otherwise it is rejected. Using probability, determine whether this is a "good" sampling plan. (Assume that a bad shipment is one that has 20 percent reds.)

The probability function for random variable X is specified as: The expected value of X is

Which of the following is not a condition of the binomial distribution?

The number of customers who enter a bank is thought to be Poisson distributed with a mean equal to 10 per hour. What are the chances that 2 or 3 customers will arrive in a 15-minute period?

The number of weeds that remain living after a specific chemical has been applied averages 1.3 per square yard and follows a Poisson distribution. Based on this, what is the probability that a 3-square yard section will contain less than 4 weeds?

The Hawkins Company randomly samples 10 items from every large batch before the batch is packaged and shipped. According to the contract specifications, 5 percent of the items shipped can be defective. If the inspectors find 1 or fewer defects in the sample of 10, they ship the batch without further inspection. If they find 2 or more, the entire batch is inspected. Based on this sampling plan, the probability that a batch that contains twice the amount of defects allowed by the contract requirements will be shipped without further inspection is approximately .3874.

Jennings Assembly in Hartford, Connecticut, uses a component supplied by a company in Brazil. The component is expensive to carry in inventory and consequently is not always available in stock when requested. Furthermore, shipping schedules are such that the lead time for transportation of the component is not a constant. Using historical records, the manufacturing firm has developed the following probability distribution for the product's lead time. The distribution is shown here, where the random variable is the number of days between the placement of the replenishment order and the receipt of the item. 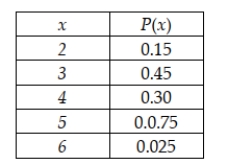What is the average lead time for the component?

Many people believe that they can tell the difference between Coke and Pepsi. Other people say that the two brands can't be distinguished. To test this, a random sample of 20 adults was selected to participate in a test. After being blindfolded, each person was given a small taste of either Coke or Pepsi and asked to indicate which brand soft drink it was. Suppose 14 people correctly identified the soft drink brand. Which of the following conclusions would be warranted under the circumstance?

The following probability distribution has been assessed for the number of accidents that occur in a Midwestern city each day: 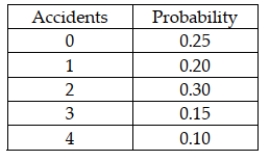The probability of having less than 2 accidents on a given day is:

Which of the following statements is true?

If the number of defective items selected at random from a parts inventory is considered to follow a binomial distribution with n = 50 and p = 0.10, the standard deviation of the number of defective parts is:

What is the difference between a discrete random variable and a continuous random variable?

Jennings Assembly in Hartford, Connecticut, uses a component supplied by a company in Brazil. The component is expensive to carry in inventory and consequently is not always available in stock when requested. Furthermore, shipping schedules are such that the lead time for transportation of the component is not a constant. Using historical records, the manufacturing firm has developed the following probability distribution for the product's lead time. The distribution is shown here, where the random variable is the number of days between the placement of the replenishment order and the receipt of the item. 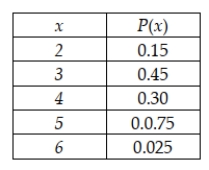What is the coefficient of variation for delivery lead time?

A corporation has 11 manufacturing plants. Of these, 7 are domestic and 4 are located outside the United States. Each year a performance evaluation is conducted for 4 randomly selected plants. What is the probability that a performance evaluation will contain 3 plants from the United States?

One of the characteristics of the binomial distribution is that the probability of success for each trial depends on whether the previous trial was a success or not.