Exam 5: Discrete Probability Distributions

If a binomial distribution applies with a sample size of n = 20, find the probability of 5 successes if the probability of a success is 0.40.

The random variable x is the number of customers arriving at the service desk of a local car dealership over an interval of 10 minutes. It is known that the average number of arrivals in 10 minutes is 5.3. The probability that there are less than 3 arrivals in any 10 minutes is:

The number of no-shows each day for dinner reservations at the Cottonwood Grille is a discrete random variable with the following probability distribution: 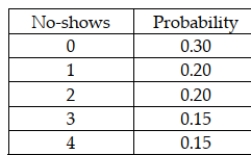Based on this information, the standard deviation for the number of no-shows is about 0.36 customers.

Explain what the expected value of a discrete random variable measures.

In a Florida town, the probability distribution for the number of legitimate emergency calls per day for the Fire Department is given as follows. Also shown is the probability distribution for the number of false alarms: 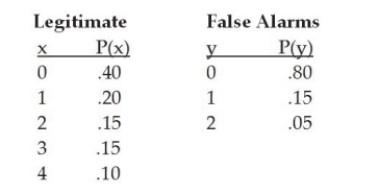Given this information, the expected number of total calls to the fire department is 1.60 calls.

The number of customers who enter a bank is thought to be Poisson distributed with a mean equal to 10 per hour. What are the chances that no customers will arrive in a 15-minute period?

The number of defects discovered in a random sample of 100 products produced at the Berdan Manufacturing Company is binomially distributed with p = .03. Based on this, the standard deviation of the number of defects per sample of size 100 is 2.91.

The makers of Crustfree Bread in Boston have a quality standard that allows for no more than 3 burned loaves per batch on average. Assuming that the average of 3 per batch is being met, the standard deviation for the number of burned loaves in 4 batches is approximately 1.73 loaves.

If the standard deviation for a Poisson distribution is known to be 3, the expected value of that Poison distribution is:

Given a binomial distribution with n = 8 and p = 0.40, obtain the probability that the number of successes is within 2 standard deviations of the mean.

The number of no-shows each day for dinner reservations at the Cottonwood Grille is a discrete random variable with the following probability distribution: 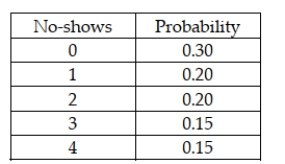Based on this information, the expected number of no-shows is 1.65 customers.

The following probability distribution has been assessed for the number of accidents that occur in a Midwestern city each day: 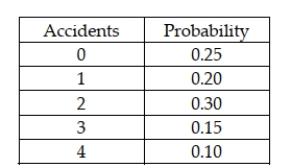Based on this probability distribution, the standard deviation in the number of accidents per day is:

The distribution for the number of emergency calls to a city's 911 emergency number in a one-hour time period is likely to be described by a binomial distribution.

The Hawkins Company randomly samples 10 items from every large batch before the batch is packaged and shipped. According to the contract specifications, 5 percent of the items shipped can be defective. If the inspectors find 1 or fewer defects in the sample of 10, they ship the batch without further inspection. If they find 2 or more, the entire batch is inspected. Based on this sampling plan, the probability that a batch that meets the contract requirements will be shipped without further inspection is approximately .9139.

The manager of a fast food store realizes that his staffing problems are a result of the variation in the number of customers that arrive at the store. If the same number of customers came each hour, she would know exactly how many servers to have working. It turns out that the Poisson distribution works well to describe the arrivals of customers in any given hour. Explain why the manager has more trouble staffing the store during those hours when the average arrival rate is higher.

A company has 20 copy machines and every day there is a 5 percent chance for each machine that it will not be working that day. If the company wants to calculate the probability of, say, 2 machines not working, it should use the Poisson distribution.

Consider a situation in which a used-car lot contains five Fords, four General Motors (GM) cars, and five Toyotas. If five cars are selected at random to be placed on a special sale, what is the probability that three are Fords and two are GMs?

A stock portfolio contains 20 stocks. Of these stocks, 10 are considered "large-cap" stocks, 5 are "mid- cap," and 5 are "small cap." The portfolio manager has been asked by his client to develop a report that highlights 7 randomly selected stocks. When she presents her report to the client, all 7 of the stocks are large-cap stocks. The client is very suspicious that the manager has not randomly selected the stocks. She believes that the chances of all 7 of the stocks being large cap must be very low. Compute the probability of all 7 being large cap.

The Weyerhauser Lumber Company headquartered in Tacoma, Washington, is one of the largest timber and wood product companies in the world. Weyerhauser manufactures plywood at one of its Oregon plants. Plywood contains minor imperfections that can be repaired with small "plugs." One customer will accept plywood with a maximum of 3.5 plugs per sheet on average. Suppose a shipment was sent to this customer and when the customer inspected two sheets at random, 10 plugged defects were counted. What is the probability of observing 10 or more plugged defects if in fact the 3.5 average per sheet is being satisfied?

Given a binomial distribution with n = 8 and p = 0.40, obtain the probability that the number of successes is larger than the mean.