Exam 5: Discrete Probability Distributions

Given a binomial distribution with n = 8 and p = 0.40, obtain the mean.

The manager for State Bank and Trust has recently examined the credit card account balances for the customers of her bank and found that 20% have an outstanding balance at the credit card limit. Suppose the manager randomly selects 15 customers and finds 4 that have balances at the limit. Assume that the properties of the binomial distribution apply. What is the probability of finding 4 customers in a sample of 15 who have "maxed out" their credit cards?

The primary application for the hypergeometric probability distribution is in situations where the sampling is done without replacement from a finite population.

Dell Computers receives large shipments of microprocessors from Intel Corp. It must try to ensure the proportion of microprocessors that are defective is small. Suppose Dell decides to test five microprocessors out of a shipment of thousands of these microprocessors. Suppose that if at least one of the microprocessors is defective, the shipment is returned. Calculate the probability that the entire shipment will be kept by Dell even though the shipment has 10% defective microprocessors.

The number of no-shows for dinner reservations at the Cottonwood Grille is a discrete random variable with the following probability distribution: 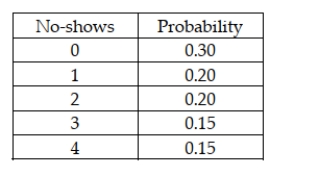Based on this information, the most likely number of no-shows on any given day is 0 customers.

Six managers at a company all enjoy golf. Each Saturday, four of the six get together for 18 holes of golf. They have decided to set up a schedule so that the same foursome does not play twice before all possible foursomes have played. The number of weekends that will pass before the same group would play twice is 15.

The manager of a movie theater has determined that the distribution of customers arriving at the concession stand is Poisson distributed with a standard deviation equal to 2 people per 10 minutes. What is the probability that 0 customers arrive during a 10-minute period?

The number of visible defects on a product container is thought to be Poisson distributed with a mean equal to 3.5. Based on this, how many defects should be expected if 3 containers are inspected?

John Thurgood founded a company that translates Chinese books into English. His company is currently testing a computer-based translation service. Since Chinese symbols are difficult to translate, John assumes the computer program will make some errors, but then so do human translators. The computer error rate is supposed to be an average of 3 per 400 words of translation. Suppose John randomly selects a 1,200-word passage. Assuming that the Poisson distribution applies, if the computer error rate is actually 3 errors per 400 words, calculate the probability that more than 14 errors will be found.

Cramer's Bar and Grille in Dallas can seat 130 people at a time. The manager has been gathering data on the number of minutes a party of four spends in the restaurant from the moment they are seated to when they pay the check. 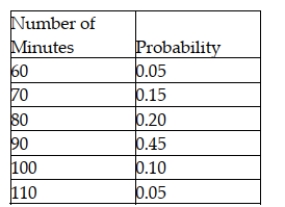What is the variance and standard deviation?

If a distribution is considered to be Poisson with a mean equal to 11, the most frequently occurring value for the random variable will be:

Bill Price is a sales rep in northern California representing a line of athletic socks. Each day, he makes 10 sales calls. The chance of making a sale on each call is thought to be 0.30. The probability that he will make exactly two sales is approximately 0.2335.

Dell Computers receives large shipments of microprocessors from Intel Corp. It must try to ensure the proportion of microprocessors that are defective is small. Suppose Dell decides to test five microprocessors out of a shipment of thousands of these microprocessors. Suppose that if at least one of the microprocessors is defective, the shipment is returned. If Intel Corp.'s shipment contains 10% defective microprocessors, calculate the probability the entire shipment will be returned.

The manager for State Bank and Trust has recently examined the credit card account balances for the customers of her bank and found that 20% have an outstanding balance at the credit card limit. Suppose the manager randomly selects 15 customers and finds 4 that have balances at the limit. Assume that the properties of the binomial distribution apply. What is the probability that 4 or fewer customers in the sample will have balances at the limit of the credit card?

If the number of defective items selected at random from a parts inventory is considered to follow a binomial distribution with n = 50 and p = 0.10, the expected number of defective parts is:

A sales rep for a national clothing company makes 4 calls per day. Based on historical records, the following probability distribution describes the number of successful calls each day: 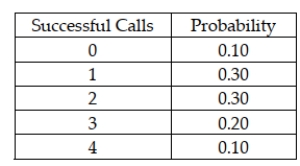Based on this information, the probability that the sales rep will have a total of 2 successful calls in a two- day period is:

The random variable, number of customers entering a store between 9 AM and noon, is an example of a discrete random variable.

The only two types of random variables are discrete and continuous random variables.

The number of customers who arrive at a fast food business during a one-hour period is known to be Poisson distributed with a mean equal to 8.60. The probability that between 2 and 3 customers inclusively will arrive in one hour is 0.0263.

The Nationwide Motel Company has determined that 70 percent of all calls for motel reservations request nonsmoking rooms. Recently, the customer service manager for the company randomly selected 25 calls. Assuming that the distribution of calls requesting nonsmoking rooms is described by a binomial distribution, the standard deviation of requests for nonsmoking rooms is 5.25 customers.