Exam 11: Hypothesis Tests and Estimation for Population Variances
Exam 1: The Where, Why, and How of Data Collection167 Questions
Exam 2: Graphs, Charts and Tablesdescribing Your Data138 Questions
Exam 3: Describing Data Using Numerical Measures138 Questions
Exam 4: Introduction to Probability125 Questions
Exam 5: Discrete Probability Distributions161 Questions
Exam 6: Introduction to Continuous Probability Distributions122 Questions
Exam 7: Introduction to Sampling Distributions136 Questions
Exam 8: Estimating Single Population Parameters174 Questions
Exam 9: Introduction to Hypothesis Testing183 Questions
Exam 10: Estimation and Hypothesis Testing for Two Population Parameters121 Questions
Exam 11: Hypothesis Tests and Estimation for Population Variances69 Questions
Exam 12: Analysis of Variance162 Questions
Exam 13: Goodness-Of-Fit Tests and Contingency Analysis105 Questions
Exam 14: Introduction to Linear Regression and Correlation Analysis139 Questions
Exam 15: Multiple Regression Analysis and Model Building148 Questions
Exam 16: Analyzing and Forecasting Time-Series Data131 Questions
Exam 17: Introduction to Nonparametric Statistics103 Questions
Exam 18: Introducing Business Analytics48 Questions
Exam 19: Introduction to Decision Analysis48 Questions
Exam 20: Introduction to Quality and Statistical Process Control42 Questions
Select questions type
In a two-tailed hypothesis test for the difference between two population variances, if s1 = 3 and s2 = 5, then the test statistic is F = 1.6667.
(True/False)
4.9/5  (41)
(41)
An analyst plans to test whether the standard deviation for the time it takes bank tellers to provide service to customers exceeds the standard of 1.5 minutes. The correct null and alternative hypotheses for this test are:
(Multiple Choice)
4.8/5  (33)
(33)
If the variance of the contents of cans of orange juice is significantly more than 0.003, the manager has to order to stop the filling machine. A sample of 26 cans of orange juice showed a standard deviation of 0.06 ounce. Based on the sample and at the 0.05 level of significance, the filling machine should be
(Multiple Choice)
4.9/5  (35)
(35)
A PC company uses two suppliers for rechargeable batteries for its notebook computers. Two factors are important quality features of the batteries: mean use time and variation. It is desirable that the mean use time be high and the variability be low. Recently, the PC maker conducted a test on batteries from the two suppliers. In the test, 9 randomly selected batteries from Supplier 1 were tested and 12 randomly selected batteries from Supplier 2 were tested. The following results were observed: 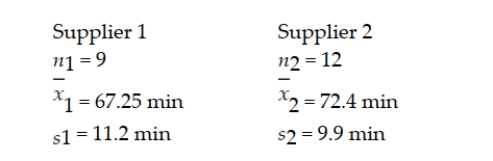 Based on these sample results, can the PC maker conclude that a difference exists between the two batteries with respect to the population mean use time? Test using a 0.10 level of significance.
Based on these sample results, can the PC maker conclude that a difference exists between the two batteries with respect to the population mean use time? Test using a 0.10 level of significance.
(Essay)
4.9/5  (36)
(36)
In a hypothesis test for the equality of two variances, the lower-tail critical value does not need to be found as long as the larger sample variance is placed in the denominator of the test statistic.
(True/False)
4.9/5  (26)
(26)
When a hypothesis test is to be conducted regarding a population variance, the test statistic will be:
(Multiple Choice)
4.9/5  (36)
(36)
Which of the following is the appropriate null hypothesis when testing whether two population variances are equal?
(Multiple Choice)
4.8/5  (32)
(32)
The Russet Potato Company has been working on the development of a new potato seed that is hoped to be an improvement over the existing seed that is being used. Specifically, the company hopes that the new seed will result in less variability in individual potato length than the existing seed without reducing the mean length. To test whether this is the case, a sample of each seed is used to grow potatoes to maturity. The following information is given:
The correct null hypothesis for testing whether the variability of the new seed is less than the old seed is:

(Multiple Choice)
4.9/5  (34)
(34)
A potato chip manufacturer has two packaging lines and wants to determine if the variances differ between the two lines. They take a sample of n= 15 bags from each line and find the following: The value of the test statistic is F = 1.5
(True/False)
4.8/5  (28)
(28)
One of the most important aspects of quality improvement is the idea of reducing the variability in a product or service. For instance, a major bank has worked to reduce the variability in the service time at the drive-through. The managers believe that the standard deviation in service time should not exceed 30 seconds. To test whether this goal is being achieved, a random sample of n = 25 cars is selected each week and the service time for each car is measured. Last week, the mean time was 345 seconds with a standard deviation equal to 38 seconds. Given this information, if the significance level is 0.10, the critical value from the chi-square table is about 34.3.
(True/False)
5.0/5  (29)
(29)
A consulting report that was recently submitted to a company indicated that a hypothesis test for a single population variance was conducted. The report indicated that the test statistic was 34.79, the hypothesized variance was 345 and the sample variance 600. However, the report did not indicate what the sample size was. What was it?
(Multiple Choice)
4.9/5  (32)
(32)
The Department of Weights and Measures in a southern state has the responsibility for making sure that all commercial weighing and measuring devices are working properly. For example, when a gasoline pump indicates that 1 gallon has been pumped, it is expected that 1 gallon of gasoline will actually have been pumped. The problem is that there is variation in the filling process. The state's standards call for the mean amount of gasoline to be 1.0 gallon with a standard deviation not to exceed 0.010 gallons. Recently, the department came to a gasoline station and filled 10 cans until the pump read 1.0 gallon. It then measured precisely the amount of gasoline in each can. The following data were recorded:  Based on these data, what should the Department of Weights and Measures conclude if it wishes to test whether the standard deviation exceeds 0.010 gallons or not, using a 0.05 level of significance?
Based on these data, what should the Department of Weights and Measures conclude if it wishes to test whether the standard deviation exceeds 0.010 gallons or not, using a 0.05 level of significance?
(Essay)
4.9/5  (37)
(37)
The null hypothesis that two population variances are equal will tend to be rejected if the ratio of the sample variances from each population is substantially larger than 1.0.
(True/False)
4.8/5  (41)
(41)
A frozen food company that makes burritos currently has employees making burritos by hand. It is considering purchasing equipment to automate the process and wants to determine if the automated process would result in lower variability of burrito weights. To conduct a hypothesis test using a 0.05 level of significance, the proper format for the null and alternative hypotheses is (where the current by- hand process is process 1 and the automated process is process 2). 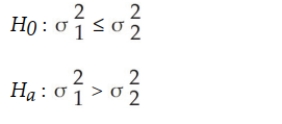
(True/False)
4.8/5  (35)
(35)
In a two-tailed test for the equality of two variances, the critical value is determined by going to the F- distribution table with an upper-tail area equal to alpha divided by two.
(True/False)
4.8/5  (29)
(29)
A fast food restaurant that sells burritos is concerned about the variability in the amount of filling that different employees place in the burritos. To achieve product consistency it needs this variability to be no more than 1.7 ounces. A sample of n = 18 burritos showed a sample variance of 2.89 ounces. Using a 0.10 level of significance, what can you conclude?
(Multiple Choice)
4.8/5  (26)
(26)
The test statistic that is used when testing a null hypothesis for a population variance is the standard normal z-value.
(True/False)
4.9/5  (34)
(34)
The F-distribution is used to test whether two sample variances are equal.
(True/False)
4.7/5  (36)
(36)
If we are interested in performing a one-tailed, upper-tail hypothesis test about a population variance where the level of significance is .01 and the sample size is n = 25, the critical chi-square value to be used is 42.9798.
(True/False)
4.8/5  (37)
(37)
A two-tailed test for two population variances could have a null hypothesis like the following: H0 : =
(True/False)
4.8/5  (29)
(29)
Showing 21 - 40 of 69
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)